一、應力集中

應力集中是在零件的截面幾何形狀突然變化處，局部應力遠大于名義應力的現象，是引起結構失效的重要力學因素，構件的主要失效部位。“革命總是在最薄弱的環節爆發”，對于結構來講，則是承受負載最大的局部區域容易失效。彈性力學研究了不同形狀的開孔對應力集中的影響程度，其中，圓孔的應力集中程度最低。由于開孔，孔口附近的應力將遠大于無孔時的應力，也大于距孔口較遠的地方。一般，圓形孔的應力集中區域在距孔邊1.5倍孔口尺寸的范圍內。在幾倍孔徑以外，應力幾乎不受孔的影響，應力分布情況以及數值幾乎與無孔時相同。因此，孔口應力集中具有局部性，通常來講集中的程度越高，集中的現象越是具有局部性。由此，應力集中不是簡單的由于截面面積減小一些而使應力有所增大，而是由于孔的存在，改變了孔附近的應力狀態和應變狀態。對于同樣形狀的孔來說，集中的程度幾乎與孔的大小無關。由于應力集中區域的應力要顯著高于其他區域，而在構件的結構強度校核中，通常需要關注的就是這些存在應力集中的高應力區域，它是確定結構所能承受多大載荷的設計依據。

從以上的分析來看，應力集中通常出現在構件空間發生突變，空間曲率或梯度發生改變的位置；若過渡區域不光滑連續，則可能會出現應力奇異。由此，構件內應力集中現象與構件空間的性質相關，對于應力集中的原因從“場”的觀點來解釋或許會更為恰當。力或應力在空間中的傳遞過程中所形成的“場”與流體相似。在“傳遞”或“流經”的路徑上，空間性質的改變將會使其產生調整，并重新分布。目前尚未查閱到深入探討相關相似問題的文獻，但相信這可能會很有趣。如果將這種應力集中的局部現象推廣到宇宙空間，會是什么樣的區域存在“應力集中”呢？“應力集中”區域會有哪些奇觀呢？

二、出現應力集中的區域

在工程實際中，由于某種用途，通常需要在構件上開孔、開槽、開缺口、制作臺階等，這些構件截面突變的區域會出現應力集中；材料本身存在的夾雜、氣孔、裂紋等非連續性缺陷也會產生應力集中；由于強拉伸、冷加工、熱處理、焊接等而引起的殘余應力，這些殘余應力疊加上工件應力后也有可能出現較大的應力集中，其中結構焊縫本身就是容易產生應力集中的部位。

文獻通過研究得出：

材料夾雜與基體彈性模量的差異越大，產生的局部應力集中也越大，氣孔導致的應力集中大于硬夾雜；

多個夾雜存在時，相鄰的應力場會發生耦合強化作用，強化效果與夾雜排列方向和加載方向有關；

在忽略夾雜的循環塑性條件下，循環應力對氣孔周圍應力集中影響較大，但對硬夾雜周圍應力集中影響很小；

氣孔非常靠近表面時，應力水平越高，應力應變集中系數Kg越大，裂紋容易在表面萌生。氣孔的位置較深時，應力水平越低，Kg越大，裂紋容易在內部夾雜處萌生。

三、應力集中的影響

受載零件上的不連續性部位（如軸肩、臺階、圓角、孔洞等）或缺陷，會嚴重影響零件的應力狀態和斷裂特征，這些不連續性部位和缺陷常常是作為應力集中的因素，萌生裂紋并形成斷裂源，表面的這些不連續因素都起到了缺口的作用。缺口越尖銳，應力集中系數越大，應力集中程度越高。缺口根部三向應力狀態的出現，是該局部應力狀態變硬，使變形受到抑制，塑性變形也被推遲到更高的水平，該現象稱為缺口強化效應。該效應與物理強化效應不同，而是一種純幾何效應。由此，缺口根部的材料行為與其他位置存在很大差異，所以缺口根部容易誘發裂紋萌生，成為斷裂源。

對于脆性材料，應力集中處的應力達到比例極限后材料開始破壞。通常裂紋是在應力集中處形成，然后更大的應力集中將產生于裂紋尖端處，這反過來引起裂紋在該截面的進一步擴展，導致材料的突然斷裂。

對于塑性材料，并承受靜態載荷時，細小的幾何缺陷、劃痕、小圓角等不需要過于擔心，設計者通常忽略應力集中系數的影響。因為此時應力超過材料比例極限并不會導致裂紋產生。反而，由于屈服和應變強化的影響，材料還有進一步承載的能力。但在動載荷或交變載荷作用下，應力集中部位是疲勞裂紋的重要發源地，降低構件的疲勞壽命。

1. 圓角

軸的圓角半徑r 與疲勞極限σ-1 之間的關系是：隨著圓角半徑r 減小，直徑d 增大，疲勞缺口應力集中系數急劇增大；反之則反。據我國某拖拉機廠統計分析了180根曲軸的疲勞斷裂案例，發現大多數斷裂時有與大修時軸徑磨削使軸徑的圓角半徑小于設計規定 (r=6) 所致，其中圓角r=1.5~3的斷軸率為70.8%，r=3~4的占18%，r=4~5的占4%。

2. 縱向溝槽

如鍵槽和花鍵等軸上的縱向溝槽，是承受扭轉應力軸件的常見失效發源地。這類失效大多數發生在尖角處，因為應力集中而萌生小裂紋造成疲勞斷裂。分析表明，鍵槽尖角引起的局部應力可達到平均額定應力的十倍。

3. 孔

軸類零件開一橫孔后，孔內側的理論應力集中系數Kt隨著d/D比值的上升而距離增大(d，橫孔直徑；D為軸向直徑)。

4. 受內壓殼體開孔接管處的應力集中

壓力容器接管處的應力集中較小孔嚴重的多，應力集中系數可達到3~6，但其應力衰減迅速，具有明顯的局部性，不會使殼體引起任何顯著的變形，故可以允許應力峰值超過材料的平均屈服應力。

5. 橢圓孔

橢圓孔無限大板，在其均勻應力垂直于橢圓長軸的情況下，最大應力發生在橢圓孔的長軸端點處，應力集中系數為Kt=1+2a/b。

6. V型缺口尖端ρ→0時

 形成一個尖銳缺口，在拉伸應力作用下，缺口尖端的應力趨于無限大，將出現所謂的奇異性。缺口尖端局部區應力可以表示為：σij∝r-1+λ；λ為奇異指數，λ與V形缺口角β有關，當β=180°時，λ=1，無缺口情況；當β＜180°時，λ總小于1，當r→0時，缺口尖端應力具有奇異性；β=0.5時，缺口轉化為裂紋，λ=0.5時，即裂紋尖端的應力奇異指數為0.5。

7. 重復缺口

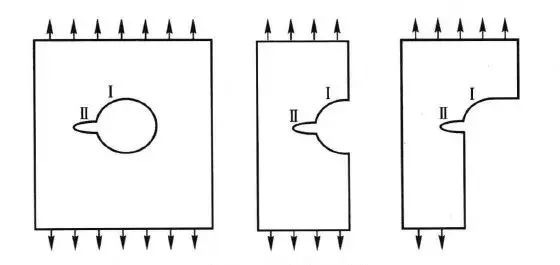
重復缺口效應是指，兩個或兩個以上的應力集中因素互相重疊而使應力集中進一步加劇的現象，如圖1所示。如果應力集中因素Ⅱ的作用遠小于應力集中因素Ⅰ的作用，則二重應力集中因素KⅠ，Ⅱ=KⅠKⅡ；如果應力集中因素Ⅱ的作用遠超過應力集中系數Ⅰ，則缺口效應主要取決于應力集中因素Ⅱ。

圖1 重復應力集中

8. 熔焊接頭

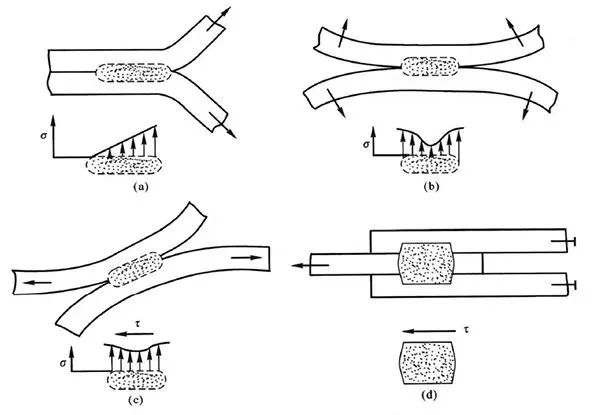
在熔焊接頭中，焊縫與母材的過渡處（焊趾）產生應力集中。焊趾是焊接接口中的典型缺口，其缺口應力可以分解為平均應力σm、彎曲應力σb和非線性應力σp。對接接頭應力集中系數的大小，主要取決于焊縫余高和焊縫向母材的過渡圓弧半徑及夾角，增加余高和減小過渡圓弧半徑，都會使應力集中系數增加。T形（十字）焊接接頭焊縫向母材過渡較急劇，其工作應力分布極不均勻，在角焊縫的根部和焊趾都存在嚴重的應力集中。搭接焊縫在只有正面焊縫的搭接接頭中，工作應力分布極不均勻，在角焊縫根部和焊趾處都有嚴重的應力集中。在用側面焊縫聯接的搭接接頭中，其工作應力更為復雜。各種焊接接頭焊后都存在不同程度的應力集中，應力集中對接頭強度的影響與材料性能、載荷類型和環境條件等因素有關。如果接頭所用材料有良好的塑性，接頭破壞前有顯著的塑性變形，使得應力在加載過程中發生均勻化，則應力集中對接頭的靜強度不會產生影響。點焊焊接接頭應力集中程度比電弧焊搭接接頭的應力集中程度嚴重，點焊接頭承受載荷時，其焊點周圍產生不同程度的應力集中，點焊接頭的抗拉強度明顯低于抗剪強度，所以在一般使用中，應盡量避免點焊接頭承受圖2所示載荷。焊接節點部位由于傳力方向改變產生復雜的結構應力，結構應力與節點焊縫的應力集中互相疊加。焊接節點的應力集中分析是焊接結構強度設計中需要考慮的重要因素，焊接缺陷是焊接結構中最嚴重的不完整性，對焊接結構承載能力有顯著的影響，并在缺陷周圍產生應力集中。

圖2 點焊承受的載荷及應力分布

四、應力集中與圣維南原理

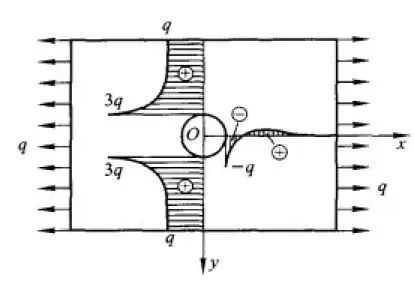
圣維南原理所描述的局部效應與應力集中存集聚之處，都是應力、應變的局部效應，但也有所區別。圣維南原理主要描述的是邊界條件等效所引起的局部應力，應變誤差的影響問題；而應力集中則主要探討構件空間突變所引起的應力集中問題。圣維南原理是在計算求解力學問題時的一個邊界簡化假設依據，且描述相對模糊；而應力集中則是力學求解的一種結果，且應力集中的局部特性可以進行量化描述。在文獻就給出了矩形板、圓形開孔的孔邊應力集成程度與距離圓孔中心遠近的關系，即一矩形薄板，在離開邊界較遠處有半徑為a的小圓孔，左右兩側受局部拉力，集度（內應力）為q，通過分析得出，應力在孔邊 (ρ=a) 是無孔時的3倍；ρ=2a時為1.22q；ρ=3a時為1.07q；ρ=4a時為1.04q。

圖3 帶圓孔矩形薄板應力集中問題

五、應力集中系數

1. 拉伸應力集中系數

理論應力集中因素等于應力集中處的最大應力σmax與該界面的平均應力σnom 的比，即K=σmax/σnom。其中，σnom=FN/A，A 是考慮截面削弱后的橫截面面積，稱為凈面積；有時平均應力的計算可以不考慮截面的削弱。理論應力集中系數K始終大于1。對于板寬超過孔徑4倍的板條，理論應力集中因素K≈3。

2. 扭轉應力集中

在工程上為了避免在軸尺寸不連續處進行復雜的應力分析，最大切應力通常可根據特定的幾何結構由一扭轉應力集中系數K 確定，τmax=KTc/J。T是截面上的合力矩，J是截面極慣性矩，c是軸的外半徑。

3. 彎曲應力集中系數

σmax=KMc/I，K是應力集中系數；M是關于橫截面中性軸的合內力偶矩，I是橫截面關于中心軸的慣性矩，c是梁外表面到中性軸的垂直距離。

應力集中系數是基于靜態加載給出的，并假設材料內部應力不能超過其本身的比例極限，材料是各向同性且均勻的。局部最大應力可以用彈性力學解析法、光彈法或有限元法求得，從而得到各種幾何形狀的試樣在各種載荷下的理論應力集中系數。常見構件形狀的應力集中系數曲線，可查閱機械設計手冊，但需要注意的是，不同的載荷和截面形式所對應的應力集中系數是不同的。

六、應力集中有限元求解的網格劃分

 有限元分析建模，網格劃分時，對于不同部位的單元可以采用不同的大小，也應當采用不同的大小。對于邊界比較曲折的部位是應力和位移變化的比較劇烈的部位，單元必須小一些；在邊界比較平直的部位、次要部位以及應力和位移變化比較平緩的部位，單元可以大一些。當結構存在凹槽或孔洞時，在凹槽或孔洞附近將發生應力集中，即該處的應力較大且變化劇烈，必須把該處的網格劃得較為緊密，以便更為貼切的描述此處的應力和應變的變化。對此，一般有兩種方法：

一種是，用疏密不同的網格劃分，在應力集中區域附近網格比較稠密，越遠越稀疏。

另一種，是子模型法，即把工作分兩步完成，第一步采用粗大網格劃分來進行初步計算，所得到的結果在遠離應力集中區域的部位是可信的，但在應力集中源附近則只能得到近似值；第二步，將臨近應力集中區域的部分從彈性體上獨立地切分出來，進行精細劃分網格，并在邊界上施加由第一步計算得出的邊界力或邊界位移等，再進行求解。

由于應力集中區域的應力在結構強度分析中的重要性。因此，獲得精準、穩定、可靠的解至關重要。在有限元分析中，則是要消除離散誤差，獲得網格無關解。離散誤差的大小同離散方程的截斷段誤差有關。在相同的網格步長下，一般來說隨著截斷誤差階數提高，離散誤差會逐漸減小。對于同一離散格式，網格加密，離散誤差也會減小。在實際計算中，應使得網格細密到即使再進一步細化網格，在工程允許的誤差范圍內數據值解也幾乎不再發生變化，此時的解則認為是網格無關解。目前大多數有限元軟件都是采用“位移法”進行求解，其中通過虛功原理和最小作用原理，最先求解的未知量就是位移。因而，若在隨著網格逐步精細化的過程中，位移結果收斂于一個有限值，而應力則是發散的，出現此類情況也可以判斷此處出現了應力奇異。

七、應力集中的預防與利用

在結構設計中，避免應力集中的一些基本措施：

避免零件兩交接部位的截面尺寸相差太大；

增大零件上過渡曲線的曲率半徑，比如加大軸徑變化處的圓角半徑；

降低承受沖擊載荷零件的剛度；

加大壓配合部分軸的尺寸或開卸載槽；

焊接結構件要避免將焊縫布置在應力集中處，對于動載荷結構尤應注意；

合理設置筋板、肋板，分散或轉移應力集中。

應力集中雖然對于承載結構來講存在不利影響，但正是由于應力集中效應，為一些功能的實現起到重要作用。比如，食品袋上的缺口，可以方便食用時撕開；易拉罐拉片周圍的壓痕所產生應力集中，以方便開罐，等等。這些有效利用應力集中效應的實際案例，對于在使用中需要破壞和去除的結構來講是有利的。

八、應力奇異與判斷

根據彈性理論在結構內部尖角處，或說非光滑連續處的應力是無限大。在使用有限元求解過程中，應力奇異具有以下特點：

單元網格越細化，越會引起計算應力無限增大，而且不再收斂；

網格稀疏不均勻時，網格離散誤差也大小不一；

添加在節點上的集中載荷與施加在與該節點相連的單元上的均布載荷相當的話，這些節點就會成為應力奇異點；

離散約束點導致非零反力的出現，就像在一個節點上施加一個集中力，這時約束點也就成為應力奇異點。但實際中，當考慮應力奇異點的區域時，這些假設都是錯誤的，只要該點受載荷，就一定有位移；

銳利的拐角處。如果模型中存在尖角（直角），那么網格的細分會改變尖角處的應力計算值，值不收斂。實際中該情況并不絕對存在。

在有限元計算分析實踐中發現，應力奇異的區域應力集中系數較高，理論上是無限大，應力集中度會很高，應力衰減明顯。因此在分析中，首先需要關注的是結構上那些不光滑連續的區域；其次，對不連續區域的鄰域進行劃分，并在網格細化，尋找網格無關解的過程，比較確認不同區域計算值的收斂程度。當不連續區域鄰域內的解已趨于收斂，且滿足誤差要求，但不連續區域的解始終差異較大時，就可以確認該區域出現了應力奇異。

九、應力奇異處理

在遇到應力奇異時，可以考慮采用以下方法進行處理：

細化模型。主要是在模型中添加細節特征（如倒角、過渡面等），再重新計算或者采用子模型法進行分析。

外插值法或路徑法。假設應力奇異在該區域沒有發生用來推斷奇異點的應力值，可使用應力集中系數來計算真實應力。

局部細化網格。在幾何尖角處，應力解梯度大的區域網格應細分，其他遠離的位置可以粗劃。如果遠離奇異點的解是收斂的，則粗糙網格也會較為準確的估計這部分的解，但對于接近奇異點的解是不可靠的。

將模型轉化為可借用理論公式計算的形式，并根據設計手冊查找該模型結構及尺寸的應力集中系數來預測真實應力。