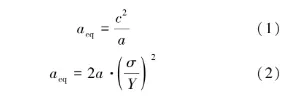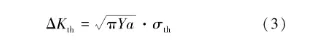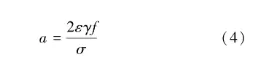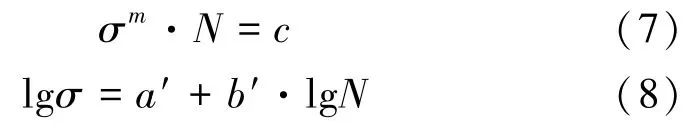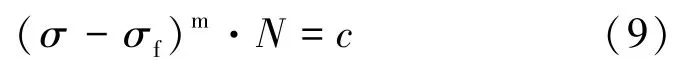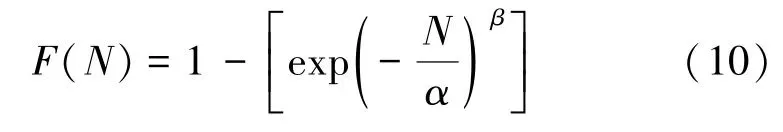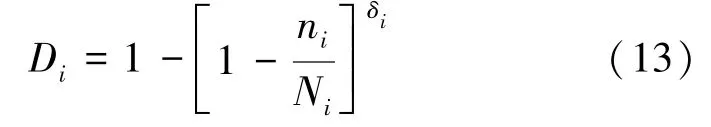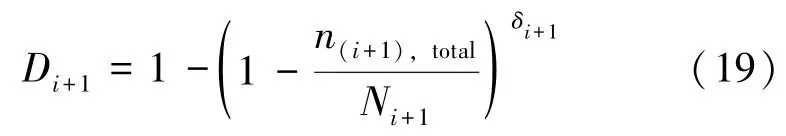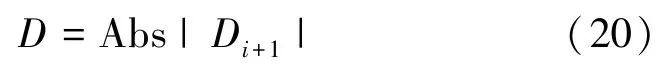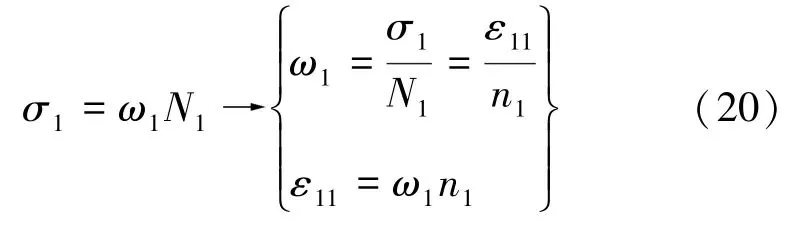引文格式 王德龍, 王明明, 李瑞升, 等. 金屬材料高周疲勞失效分析及仿真模擬研究進展[J]. 塑性工程學報, 2025, 32 (1):16-29. WANG Delong, WANG Mingming, LI Ruisheng, et al. Research progress of high-cycle fatigue failure analysis and simulation of metal materials [J]. Journal of Plasticity Engineering, 2025, 32 (1):16-29.
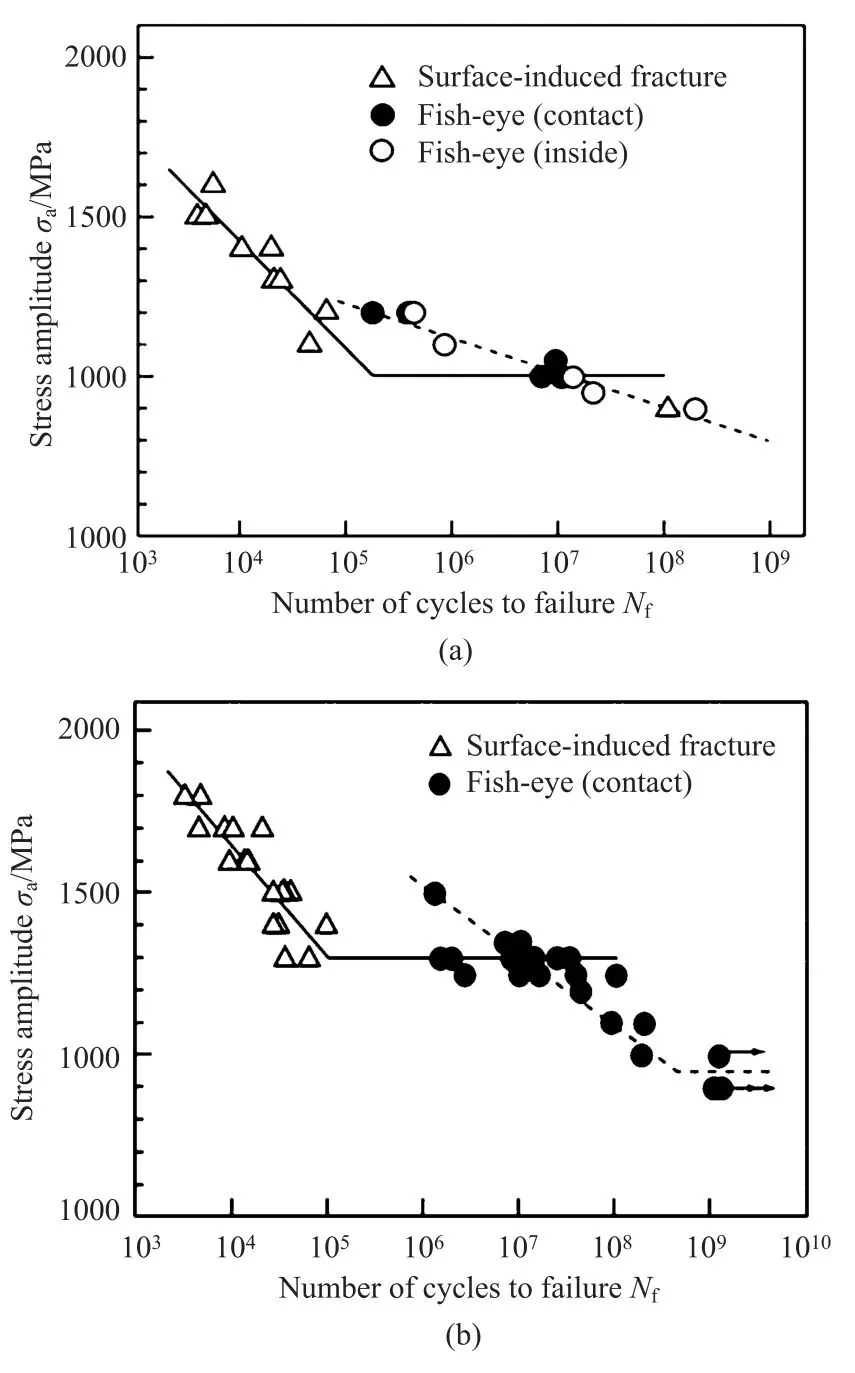
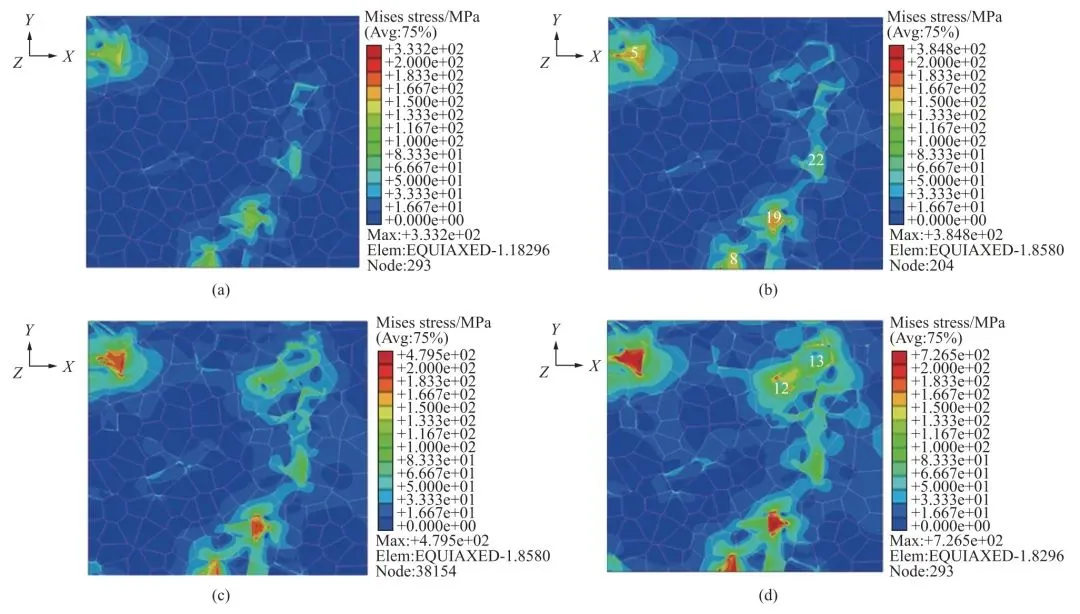
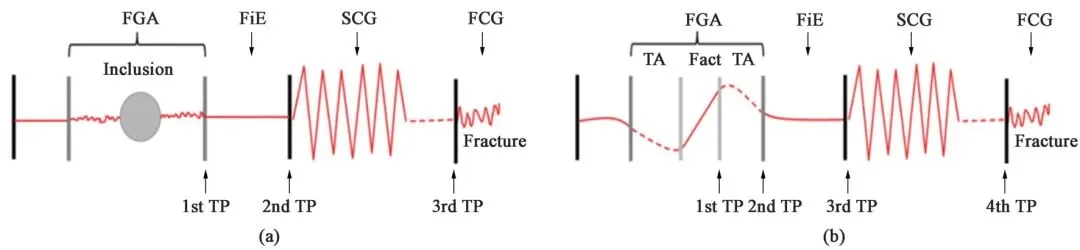
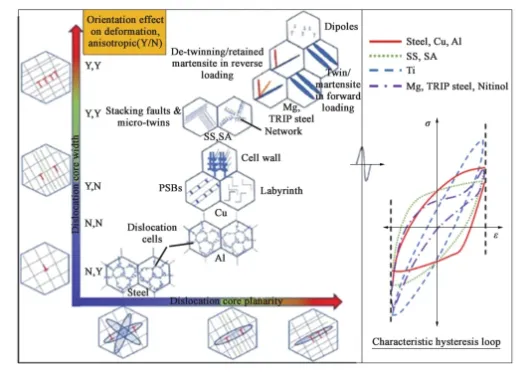
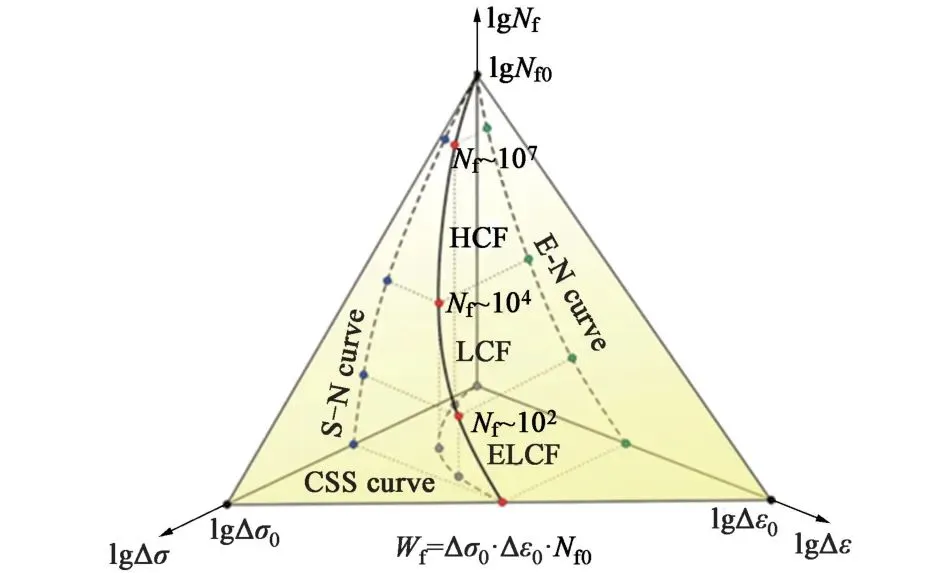
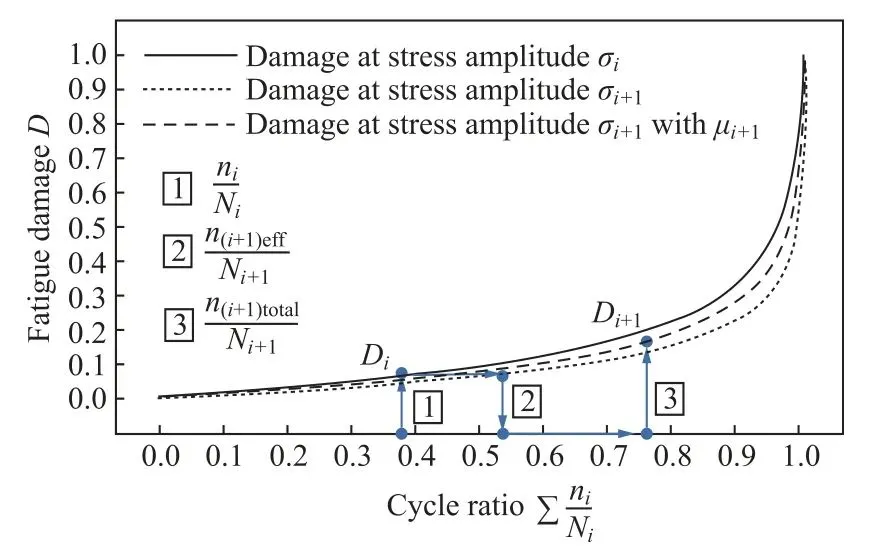
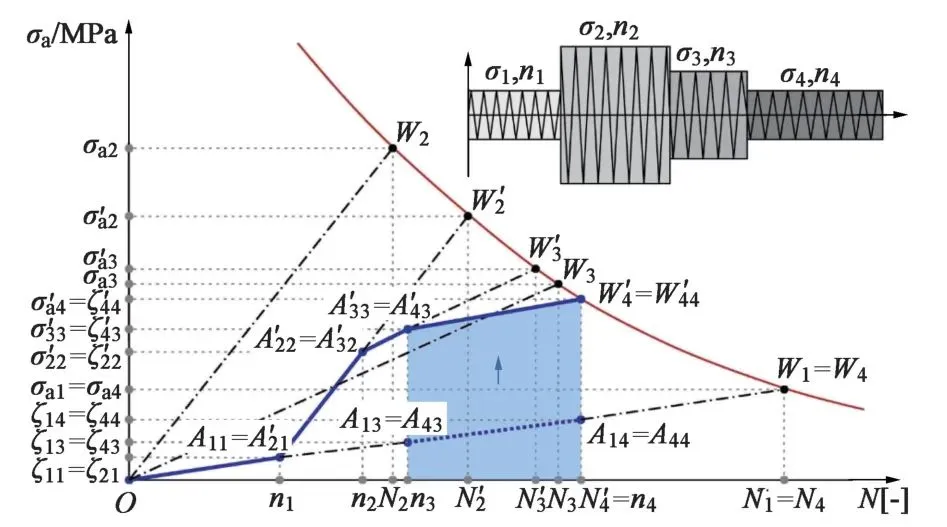
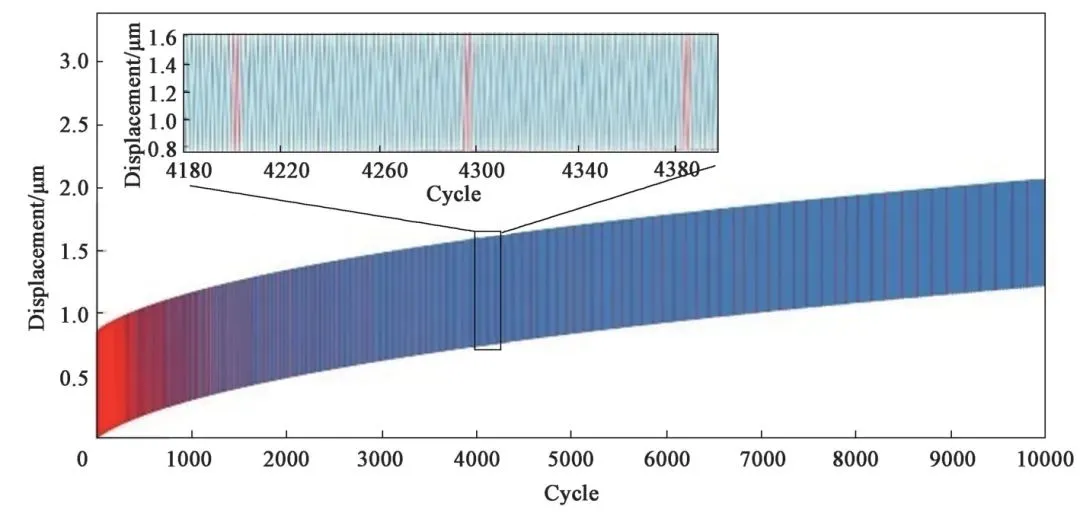
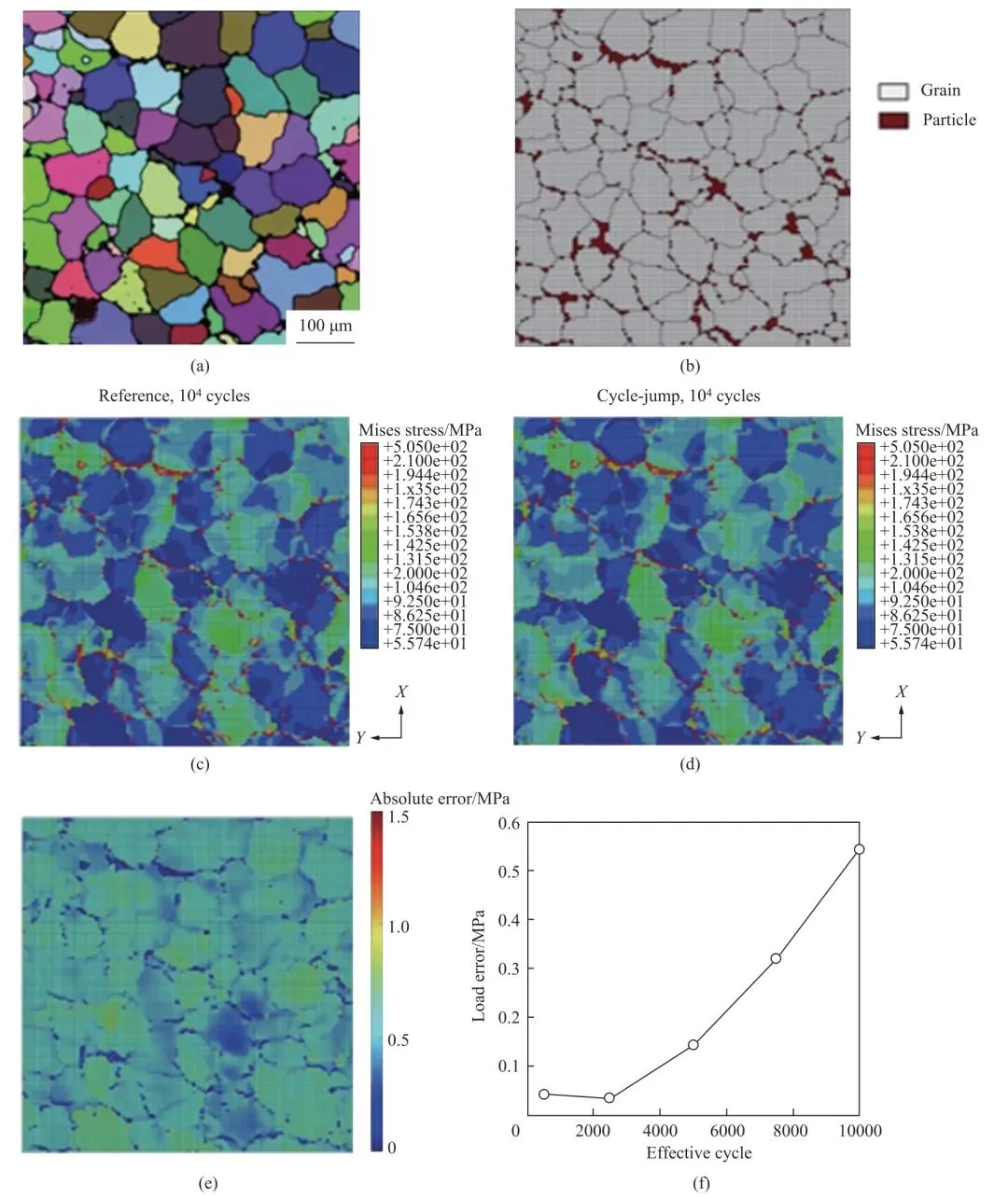
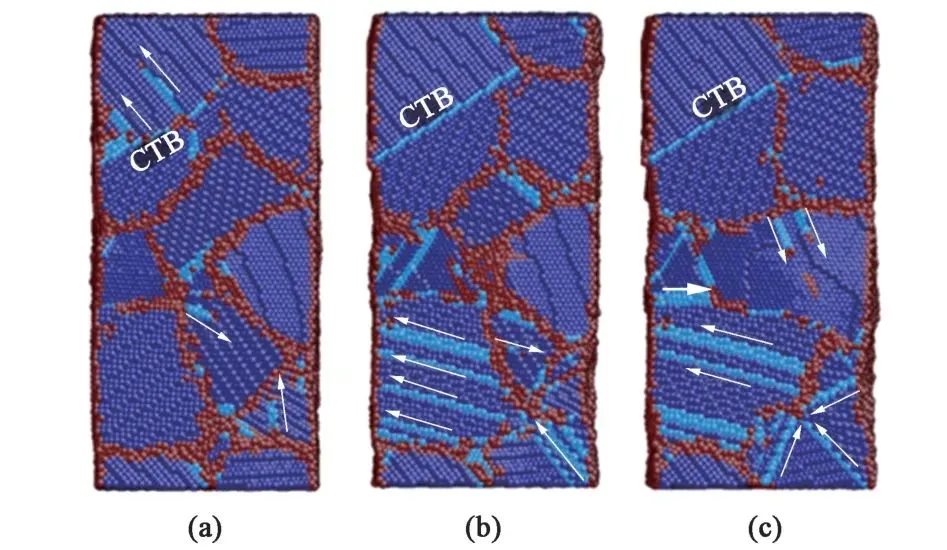
王德龍1, 王明明1, 李瑞升1, 張曉妍2, 李冬冬1, 紀宏超1, 張好強1 (1.華北理工大學 機械工程學院;2.華北理工大學 冶金與能源學院) 摘 要:金屬材料高周疲勞失效是機械工程領域中一種極為重要的失效形式, 也是引起惡劣安全事件的重要原因。為了深入研究金屬材料的高周疲勞過程、疲勞壽命的影響因素及疲勞過程中的組織演變規律等, 疲勞實驗、 斷口分析和組織表征等手段已被引入疲勞失效分析, 此外, 為了縮減實驗周期, 并且能夠對疲勞過程進行表征, 還產生了多種高周疲勞預測、仿真模型。因此,本文在匯總金屬材料高周疲勞失效特征、失效機理的基礎上, 著重對高周疲勞的預測方法、仿真方法和數學模型進行了闡述, 旨在為深入理解和預測金屬材料的高周疲勞性能提供參考。 關鍵詞:高周疲勞;疲勞性能預測;疲勞模擬 引言 高周疲勞(High Cycle Fatigue, HCF) 是工程領域中的一個重要問題, 特別是在航空、 汽車和機械制造等行業中受循環載荷的零部件, 因循環載荷造成的累積損傷更易使其發生疲勞破壞。隨著工程結構輕量化要求和服役環境的嚴苛性, 金屬材料在高周循環載荷下的性能和壽命變得更為關鍵。并且隨著高周疲勞循環次數的增加, 金屬材料顯示出了不同于低周疲勞的損傷、 失效行為, 這給材料設計和結構壽命評估帶來了挑戰。為了解決金屬材料高周疲勞失效機理問題, 科研人員持續探索了不同的測試、 表征方法和技術, 其中包括材料表征、 數字仿真模擬和實驗驗證等。 本文總結了金屬高周疲勞性能及模擬的研究進展, 分析了當前高周疲勞研究存在的問題, 討論了材料表征方法、 仿真模型和實驗技術的發展, 并探討其應用在工程實踐方面的潛力。此外還提出了未來金屬高周疲勞研究的方向和挑戰, 以促進該領域的進一步發展和創新。為金屬材料高周疲勞性能及模擬研究提供參考, 以及相關工程實踐提供科學依據和技術支撐。 1.高周疲勞失效特征 高周疲勞是機械工程領域中一種常見的疲勞失效形式, 具有以下幾個特征。 (1) 高周疲勞是在高周次循環載荷下發生的。材料在每個循環載荷的作用下都會經歷應力、 應變的變化。循環次數的增加會導致位錯增值, 產生應力集中現象, 出現循環強化或軟化, 最終導致材料逐漸接近疲勞極限。與其他疲勞形式相比, 高周疲勞壽命通常在105~107循環次數。在疲勞失效過程中, 不同的疲勞類型存在著不同的破壞機理, 如圖1所示。對于高強鋼而言, 如果材料在低周階段就己經發生疲勞失效, 則其疲勞失效源通常位于材料表面, 如加工引起的刀痕等; 若材料在高周階段發生疲勞失效, 則疲勞失效源通常位于材料內部, 如內部夾雜物等。 圖1 不同疲勞類型的S-N曲線(a) 軸向加載疲勞 (b) 旋轉彎曲疲勞 (2) 高周疲勞屬于彈性疲勞。在高周疲勞中,材料在每個循環中都會回彈到原始狀態, 沒有塑性變形。這表明在高周疲勞破壞發生前, 材料通常不會出現明顯的變形。最后, 高周疲勞的破壞通常是突然發生的。在經歷大量循環后, 材料的疲勞壽命達到極限, 出現裂紋并最終導致失效。與靜態加載下的破壞不同, 高周疲勞失效往往沒有明顯預兆, 很難通過外觀檢查等方法提前發現。因此了解高周疲勞的特征對于機械生產來說至關重要, 可以幫助設計和評估材料和結構的疲勞壽命, 以保證產品的可靠性和安全性。 2.高周疲勞失效機理 在高頻載荷往復加載下, 材料內部發生微小、反復的彈性變形, 進而形成應力集中區域。這些應力集中區域可以導致材料局部塑性變形, 產生微小裂紋。這些裂紋在應力周期的作用下, 擴展并逐漸增長, 直至達到臨界尺寸, 導致材料的斷裂。下文將對在高周疲勞失效模式中起重要作用的相關因素進行討論。 2.1 應力集中 高周疲勞失效通常在應力集中的位置發生。細小裂紋或夾雜物周圍的應力集中會導致材料局部應力增加, 從而加速裂紋的形成和擴展。通過研究孿生誘發塑性 (Twinning Induced Plasticity,TWIP) 鋼的高周疲勞行為, LIU R等發現位錯可以在夾雜界面處形成位錯堆積, 導致高應力集中,因此夾雜物界面是微裂紋形核的潛在位置; 而孿晶界處的應力集中較低, 因此孿晶界不能作為微裂紋萌生的場所。BELYAEV M S 等研究了由低碳單晶難熔鎳合金制成的缺口試樣的高周疲勞, 缺口位置處應力集中導致HCF 限值顯著降低, 這表明應力集中是材料提前疲勞失效的一大因素。 TANG B 等開發的條件概率等效熵模型(Conditional Probability Equivalent Entropy Model,CPFE) 成功捕捉到了高周疲勞加載條件下應力集中現象。圖2為不同應力水平下HCF 加載100次后微觀結構中的Mises 應力分布。 圖2 不同應力水平下100 次循環加載后的應力分布(a) 300 MPa (b) 350 MPa (c) 400 MPa (d) 450 MPa 從圖2a和圖2b可以看出, 當應力水平為300和350MPa 時, 應力集中主要存在于晶粒5#、8#、19#和22#, 而當應力水平增加到400和450MPa時, 晶粒12#和13#周圍的應力集中明顯增加, 這些晶粒的共同特點是其施密特因子較大, 微塑性累計較多。此外, 可以觀察到最大應力位置隨應力水平的變化而變化。因此應力集中是高應力水平HCF加載條件下一個重要的疲勞指標參數。 2.2 微觀缺陷 微觀缺陷如夾雜物、晶界和位錯等, 對高周疲勞失效起著重要作用。在夾雜物含量基本相同的條件下, 夾雜物的大小、 形狀及分布特征對疲勞壽命都具有明顯的影響, 夾雜物的尺寸越大, 越容易成為裂紋萌生的起點。夾雜物尺寸等效微裂紋尺寸的式通常采用Griffith 能量平衡原理, 即在相同應力下等能耗原理。當夾雜物處于邊界表面和夾雜物內部時, 夾雜物尺寸a 和等效微裂紋長度aeq的關系分別如式(1) 和式(2) 所示。 基于材料的微觀缺陷特征, Murakami 模型提供了一種方法, 用于評估夾雜物尺寸與疲勞壽命之間的關系: 當夾雜物的平均尺寸大于40μm時, 式(3)不再適用, 這種情況下可以使用Griffith 破裂力學模型, 式(4) 描述了夾雜物尺寸與夾雜物含量之間的關系: 從式(4) 可以看出, 夾雜物含量越多、 材料的表面能越小以及應力越大,夾雜物尺寸增大, 從而對材料的強度產生更大的影響。 通過式(1) ~式(4)可以預估夾雜物的尺寸和裂紋大小之間的關系以及其對材料的疲勞壽命影響。需要注意的是, 實際情況還受到材料的內在差異、 應力分布、 夾雜物的形狀以及材料本身的疲勞強度等因素的影響, 需要結合實驗數據進行綜合分析。雖然夾雜物尺寸大于40μm時, 由夾雜物引起的疲勞失效比率可達95%以上, 但目前也可以通過真空冶煉、電渣重熔以及精煉爐熔煉等冶金技術將夾雜物尺寸控制在1μm以下。不同類型夾雜物會誘發產生不同的斷裂行為, WANG P 等在研究高碳鉻軸承鋼疲勞裂紋時發現, 夾雜物誘發軸承鋼疲勞斷裂分為基體與氧化物夾雜物界面處產生疲勞斷裂以及氮化物夾雜物內部產生疲勞斷裂, 如圖3所示。圖3a中的疲勞斷裂源是Al2O3, 圖3b中氧化物夾雜物完全從基體界面剝離, 由于共軛形貌在裂紋原點處保留有來了孔洞, 從而導致疲勞斷裂。圖3d和圖3e所示的同一試樣在疲勞破壞原點處的共軛形貌相同, 說明疲勞失效根源在于基體內部的氮化物夾雜物。 圖3 疲勞破壞起始處夾雜物的SEM圖像和疲勞裂紋模式示意圖 作為微觀缺陷, 晶界作為位錯產生的重要來源,在循環載荷作用下, 位錯會在晶界處增殖、堆積。TWIP鋼歷經104和106周次后疲勞試樣的掃描透射電子顯微鏡(Scanning Transmission Electron Microscopy, STEM) 圖像如圖4所示, 其中圖4a~圖4c為經過104次循環的疲勞試樣的STEM圖像。圖4a為同一晶界處的兩個位錯源, 它們具有相同的滑移體系。圖4b顯示位錯是由兩種不同的滑移體系產生的, 這兩種滑移系統對應于同一晶粒不同晶界處的兩種不同位錯源。圖4c中位錯會跨越孿晶界并在退火孿晶內部滑動。圖4d~圖4f 為106次循環疲勞試樣的STEM圖像, 顯示了晶粒內部密集的位錯纏結和位錯胞。 圖4 TWIP鋼歷經104和106次后疲勞試樣的STEM圖 2.3 裂紋的形成與擴展 在循環加載下, 裂紋逐漸形成并擴展, 最終導致構件失效。裂紋在循環載荷下的形核和擴展是通過壓力的變化引起的, 當應力達到裂紋擴展臨界值時, 材料中的裂紋就會擴展。GAO G 等通過對4種不同夾雜物尺寸和組織的研究, 探究了圖5所示夾雜誘發裂紋萌生(Inclusion Induced Crack Initiation, IICI) 和非夾雜誘發裂紋萌生(Non-Inclusion Induced Crack Initiation, NIICI) 方式。 圖5 斷口形貌 (a) 表面夾雜物 (b) 內部夾雜物 (c) NIICI斷口 (d) 放大圖與EDS分析圖 圖5a中裂紋萌生是由表面夾雜物引起的, 而圖5b由于內部夾雜物導致了裂紋萌生, 可以觀察到顆粒狀亮面(Granular Bright Facet, GBF)。圖5c 中非夾雜物誘導斷口形成了魚眼區(Fish Eye, FiE)。圖5d中的十字表示EDS聚集區域, 通過詳細的EDS分析表明, 非夾雜物誘導的GBF周圍不存在夾雜物, 其成分與基體相似, 這證明了裂紋的起裂是由內部微觀組織引起的, 而非夾雜物。 GUI X 等和FAN Y等通過對IICI 和NIICI斷口特征區的三維觀察和計算, 證實了含夾雜物較大的試樣主要由夾雜物誘發疲勞裂紋, 而微觀組織較粗的試樣則主要由組織內部誘發疲勞裂紋, 如圖6所示, 其中TA為過渡區, FGA為細粒區,SCG表示裂紋穩定擴展, FCG表示裂紋快速擴展,TP為過渡點。 圖6 裂紋萌生斷裂示意圖(a) 夾雜誘導裂紋萌生 (b) 非夾雜誘導裂紋萌生 由圖可知, 夾雜物周圍形成應力集中, 在其周圍形成細顆粒區, 進而誘導裂紋萌生, 然后裂紋進一步擴展形成魚眼區, 最終裂紋快速擴展直至斷裂,如圖6a所示。非夾雜物誘導裂紋的形核和早期擴展發生在含有微面和周圍TA 的GBF區域內, 其后續裂紋擴展與斷裂過程與IICI大致相同, 見圖6b。 2.4 微觀結構的變化 高周疲勞加載導致材料微觀結構的變化, 如位錯增殖、晶體滑移、形成亞晶等, 這些微觀結構的變化會對材料的疲勞行為產生影響, 一方面增加了材料的強度, 即循環硬化, 另一方面也可能導致疲勞裂紋的形成和擴展。多次反復的加載和卸載會導致載荷重新分配到材料內部微觀結構中具有不同強度的相、 孔隙以及靠近嚴重取向錯誤晶粒邊界的區域。這些位置的變形和應力集中會導致微小裂紋的形核, 而這些微小裂紋又會進一步擴大, 最終導致材料結構的完全破壞。近年來, 許多研究工作也都集中在通過改善材料的微觀結構來提高部件的使用壽命。如通過激光或超聲表面改性來延緩表面裂紋的激發, 或通過電子束熔化增材制造技術來針對特定的位置直接設計、打印具有復合微觀結構的材料, 或調整貝氏體鋼種殘余奧氏體的形態來抑制疲勞裂紋的萌生。 由于晶界效應的存在, 多晶材料的單晶變形表現有明顯不同。在低周疲勞條件下, 局部應力-應變與整體應力-應變存在較大差異。在循環應力/應變的周期性作用下, 組織中形成了高、 低位錯密度域和孿晶的三維周期性結構, 如圖7所示。Fe、Co和W等BCC金屬通常具有非平面位錯芯結構,其位錯芯寬度較窄, 導致形成三維位錯胞。FCC金屬如Al、Cu等, 雖為平面位錯芯, 但由于層錯能高, 位錯芯同樣較窄, 也形成三維位錯胞。對于層錯能中等的FCC 金屬, 其最常見的特征是二維位錯結構隨晶粒取向的不同而變化; TWIP 鋼和鎳基高溫合金等低層錯能的FCC 金屬, 形成位錯網絡、 層錯和微孿晶; 這些位錯和孿晶結構會對疲勞裂紋的形成產生影響。Mg、Ti 和Zn 等HCP金屬由于具有較寬的位錯芯結構,往往形成不同取向的孿晶結構。 圖7 循環變形金屬材料的亞結構示意圖 循環載荷作用下, BCC金屬中原子發生位錯和斷裂引起疲勞失效。疲勞裂紋往往與晶粒邊界和非金屬夾雜物相互作用, 這些缺陷與位錯相互作用導致晶粒內的斷裂。相較于BCC結構金屬, FCC金屬具有較長的疲勞壽命, 其失效機理包括滑移和斷裂。晶體中的原子通過滑移形成位錯, 導致原子與晶體中的鄰近原子之間發生相對位移。而疲勞裂紋通常形成于滑移位錯的交叉點, 也可以從非金屬夾雜物周圍開始。在加載過程中, 這種位錯會在加載過程中積累并最終導致斷裂。HCP金屬在加載過程中, 晶體中的原子通過滑移形成位錯, 并會在某個特定的晶體面上形成孿晶。這些位錯和孿晶會導致材料的強度下降和疲勞裂紋的形成, 此外疲勞裂紋可以在各個晶粒之間傳播。 總的來說, 疲勞失效機理是一個復雜的過程,涉及到多個因素的相互作用。材料中的缺陷、微觀組織結構以及表面特性、外界環境等都會對疲勞行為產生影響。為了延緩高周疲勞失效, 在工程實踐中可以采取一些措施, 如優化材料的強度和韌性、減少應力集中、 改善材料的表面質量、 進行適當的設計和材料選擇等。同時需要通過實驗、數值模擬和理論分析等手段, 深入研究高周疲勞失效機理,以提高材料的疲勞壽命和可靠性。 3.高周疲勞性能預測 數值模擬方法是金屬高周疲勞性能預測的主要方法, 包括有限元分析、 晶體塑性模擬、分子動力學模擬等。通過材料的力學和物理性能的數學模型,結合適當的邊界條件和加載條件, 來模擬材料在高頻應力環境下的變形、應力分布和疲勞壽命。張哲峰等對疲勞性能預測模型進行了統一的探索, 并得到了以應力幅Δσ、 應變幅Δε 與疲勞壽命Nf為X、 Y 和Z軸的三維正交坐標系的金屬材料疲勞性能統一模型, 如圖8所示。 圖8 金屬材料疲勞性能統一模型 該三維疲勞模型全面涵蓋了應力、 應變與能量等疲勞性能評價方式, 從根本上解決了應力/應變等單一衡量標準所引發的分歧, 并由此構建出疲勞性能統一理論的雛形。下面介紹幾種實現高周疲勞壽命預測的方法。 3.1 經驗式法 經驗式法基于大量實驗數據和經驗總結, 建立數學式來預測材料的疲勞壽命。常見的經驗式包括Wöhler 式、 Coffin-Manson式等。這些式基于一定的假設和經驗規律, 適用于特定材料和載荷條件下的疲勞壽命預測。例如, S-N曲線法是一種常見的經驗式法, 通過繪制應力振幅和循環次數之間的對數曲線來預測壽命。這種方法適用于已有大量實驗數據和經驗式的情況。 S-N曲線表達式主要為以Wöhler 式為代表的指數函數形式: 對式(5) 取對數如下: 同樣在描述應力壽命式時還可以運用非常普遍的冪函數式Basquin模型: 將Stromeyer 模型引入疲勞極限σf可得: 威布爾(Weibull) S-N 曲線描述了材料在不同應力水平下的壽命分布: 3.2 確定性分析法 確定性分析方法是一種基于材料和幾何特性的疲勞壽命預測方法。通過收集材料的力學性能數據、實驗數據和幾何尺寸等參數, 結合疲勞壽命式和理論模型, 進行數值計算來估計高周疲勞壽命。這種方法需要較為準確的輸入數據和較復雜的計算模型,適用于對于特定材料和幾何形狀的預測。在給定裂紋范圍內, 高周疲勞壽命的估計方法是將材料的裂紋擴展阻力定義為裂紋長度的函數, 假設施加的驅動力與材料裂紋擴展阻力之間的差值定義了施加在裂紋上的有效驅動力。CHAPETTI M D等對表面裂紋和內部夾雜裂紋的疲勞裂紋擴展壽命進行了評估和分析。通過已知材料的裂紋擴展速率作為有效驅動力的函數, 估計出給定裂紋長度范圍內的高周疲勞壽命, 圖9a為施加應力幅為900MPa時內部裂紋對應的裂紋擴展速率與裂紋長度的關系。 圖9 確定性分析法 已知控制體積首次被MURAKAMI Y等提出,用以解釋軸向拉伸、壓縮載荷與扭轉載荷下材料疲勞強度比降低現象, 圖9b為隨載荷類型及試樣尺寸變化的S-N曲線。在此基礎上, CARPINTERI A等通過考慮結構反應截面的分形特性, 應用分形方法解釋了疲勞強度隨試樣尺寸增大而降低的現象。高周疲勞狀態下試樣尺寸對金屬材料疲勞壽命同樣有影響, SUN C等提出了一種全新的統計分析方法探究其中的聯系。首先將大型試樣的性能與小型試樣的性能通過控制體積相關聯, 通過模擬發現結果與高周疲勞狀態下的一系列實驗數據吻合較好。該方法有助于從小試件的實驗數據中定量估計大試件的疲勞壽命, 如圖9c所示。SHIRANI M 等采用最弱鏈接法研究了試樣尺寸對球墨鑄鐵高周疲勞性能的影響, 發現在獲得大試樣的P-S-N 曲線時,如圖9d 所示, 采用威布爾最弱環節法體積式比采用表面式得到的效果更好。 3.3 累計損傷法 損傷累積法是一種通過監測和累積疲勞損傷來預測壽命的方法。該方法包括疲勞損傷累積理論和壽命預測模型。通過收集疲勞損傷的相關數據, 如裂紋擴展速率、 裂紋長度等, 結合材料的疲勞行為, 可以使用損傷模型來預測高周疲勞壽命。累積疲勞損傷計算的概念可以追溯到20世紀20年代, MINER M A提出了同樣的假設, 現在被廣泛稱為Palmgren-Miner 規則、 線性損傷規則, 或者簡稱為Miner 法則。Miner 法則基于疲勞損傷等于累積循環比的假設, 如式(11) 所示。 為了更可靠地估計可變振幅載荷下的高周疲勞壽命, AERAN A 等[22]考慮了荷載序列和荷載相互作用效應, 提出了一個新的相互作用因子μ。對于加載塊i+1, 相互作用因子計算如式(12) 所示。 為了解材料在等幅加載條件下的非線性疲勞損傷演化規律, AERAN A 等提出了新的損傷指標,如式(13) 所示。假設一種材料在載荷水平i下承受一定的應力幅值δi, 循環次數為ni, 可由材料的S-N 曲線確定這種應力狀態下得循環次數為Ni。該應力范圍內的疲勞損傷可以用所提出的損傷模型來確定, 如式(13) 和式(14)。疲勞損傷D 可以用Di的絕對值表示, 如式(15) 所示。 在提出的損傷傳遞概念中, 使用荷載相互作用系數μi, 將相同的損傷傳遞到下一個應力幅值σi+1。這樣有效循環次數n(i+1),eff對應于應力范圍σi+1, 可由式(16) 和式(17) 確定。如果應力范圍σi+1的有效循環次數從一開始就存在, 則會產生相同的損傷Di: 應力狀態σi+1的循環次數為ni+1, 則加載步驟i+1的總循環次數可由式(18) 表示: 則加載步驟i+1時的累積損傷為: 相應的疲勞損傷可由式(20) 確定: 這種損傷傳遞一直持續到疲勞損傷D為1, 即疲勞失效。AERAN A等提出的損傷傳遞概念如圖10所示。該模型可以通過使用設計標準中定義的適當的S-N曲線應用于設計細節, 從而更容易地應用于實際工況中。 圖10 損傷轉移概念圖 基于雙線性S-N圖中的線性化損傷增長曲線,THEIL N提出了一種新的疲勞壽命預測模型, 該模型的目標是考慮應力水平約為0.2%屈服強度水平和略高于10%的過載塊的影響。如圖11 所示, 壽命預測方法基于迭代計算, 由4 級塊加載, 其特征為(σai, ni)。虛線表示線性化的損傷累計曲線,其斜率為相應的應力。當疲勞壽命與當前應力水平的損傷累計曲線相關時, 即第i 個載荷塊的疲勞壽命達到極限, 就會發生失效。 圖11 線性化損傷增長曲線方法在4級塊加載情況下的疲勞壽命中的應用 THEIL N假設損傷在恒定振幅下呈線性增長。圖11中OW1表示在第一個荷載水平下的損傷增長曲線。這條直線的方程可以寫成: 3.4 數值模擬法 高周疲勞模擬是通過計算機模擬方法來預測金屬材料在高頻循環載荷下的疲勞壽命、 疲勞穩定性和裂紋擴展等性能。高周疲勞性能的模擬方法主要包括宏觀模擬法、 微觀模擬法及粒子模擬法等,這些方法在分析金屬結構在高頻循環載荷下的疲勞壽命、疲勞穩定性和裂紋擴展速率等問題方面都具有一定的應用。 3.4.1 宏觀模擬法 有限元法(Finite Element Method, FEM) 是一種宏觀模擬方法, 可以用于分析和預測金屬結構在高周疲勞載荷下的疲勞壽命和疲勞損傷行為。該方法基于將結構離散為有限個單元, 并在每個單元內使用適當的數學模型進行力學分析。通過施加不同的載荷循環, 并結合材料疲勞性能數據, 可以得到結構的疲勞壽命和疲勞裂紋擴展情況, 通常用于模擬大尺度問題的行為和響應。為獲得高周疲勞過程中的可靠數據, GONCALVES L A 等使用有限元方法對特定級別的孿晶誘導塑性鋼的基于剛度演化的快速疲勞實驗進行了數值再現。孫秋秋等提出了一種基于3D內聚力有限元模擬的方法, 結合蒙特卡羅方法, 用于模擬粗晶和納米結構金屬在拉伸載荷下的疲勞裂紋萌生和擴展過程。 擴展有限元法(Extended Finite Element Method, XFEM) 是在傳統有限元離散化網格中引入額外的局部自由度, 使得有限元可以更加準確地模擬復雜的幾何形狀和局部變化, 其核心思想是通過在有限元離散化網格中引入擴展函數來擴展有限元的適用范圍。這些擴展函數可以用來表示裂紋、 接觸和界面等復雜幾何形狀。與傳統有限元方法相比,XFEM方法能更好地描述和模擬材料的非連續性、斷裂、 局部變形等現象。基于此, NIKFAM M R P等對T 型焊接接頭進行三點彎曲實驗, 得到了試樣斷口的宏觀圖, 見圖12c。然后在T型焊接接頭中插入半橢圓形XFEM 裂紋, 結合Abaqus 對鋼制T型接頭進行高周疲勞模擬。結果顯示數值模型得到的斷口形貌與實驗形貌基本吻合。此外, XFEM 對裂紋擴展、 裂紋擴展速率、 失效循環次數、裂紋形狀和最終裂紋尺寸的預測結果與實驗結果相當。 圖12 T 型焊接接頭(a) 有限元分析 (b) 高周疲勞實驗 (c) 試樣斷口宏觀圖 (d) 斷裂表面三維視圖 邊界元法 (Boundary Element Method, BEM)是另一種常用的宏觀模擬方法, 適用于求解固體結構的邊界條件問題。邊界元方法將問題的邊界離散化為多個網格單元, 并通過求解邊界積分方程來計算結構的響應。對于高周疲勞性能的模擬, 邊界元方法可以用于分析結構的疲勞壽命和裂紋擴展速率等。它將問題的邊界離散化成網格單元, 并通過求解邊界積分方程計算結構的響應。它的優點是可以避免體積元方法的小尺寸效應, 同時對結構的疲勞裂紋擴展速率有較好的預測。 3.4.2 微觀模擬法 晶體塑性模擬 (Crystal Plasticity Simulation,CPM) 是基于晶體塑性理論, 模擬晶體的變形和塑性行為, 研究材料在微觀尺度下的塑性形變、 預測微觀組織與力學性能關系的有效方法。晶體塑性模型被開發出來用以描述高周疲勞加載下的滑移活動行為和損傷形成。 如圖13所示, CHENG J 等基于微觀結構的高周晶體塑性有限元模擬, 提出了一種效率更高且實施更加簡單的循環跳躍加速方法, 首先采用常規CPFE 方法作為參考和循環跳躍法進行荷載控制循環塑性模擬的位移比較, 發現加速結果與參考結果吻合較好。該團隊將電子背散射衍射 (Electron Backscatter Diffraction, EBSD) 圖像得到的Al-Cu-Mn-Zr (ACMZ) 鋁合金的微觀結構轉化為了有限元模型, 通過比較局部應力和內部變量的演變來檢驗循環跳躍方法的準確性。圖14c和圖14d分別描述了參考結果和循環跳躍結果在104次循環下的應力分布, 圖14e為兩種方法絕對誤差, 整個微觀組織的最大絕對誤差僅為1.5MPa。圖14f是通過平均絕對誤差所繪制為有效周期的函數。在較高的循環次數下, 誤差仍小于0.6MPa, 小于施加應力的0.5%, 證明了該模型的可靠性。 圖13 常規CPFE 方法與循環跳躍法載荷控制循環塑性模擬的位移比較 圖14 ACMZ 微觀結構及模擬結果對比圖(a) EBSD 圖像 (b) 有限元網格 (c) CPFE 法模擬結果(d) 循環跳躍加速法模擬結果 (e) 兩種模擬結果的絕對誤差 (f) 荷載誤差圖 3.4.3 分子動力學模擬 分子動力學模擬 (Molecular Dynamics, MD)基于分子動力學算法, 模擬原子或分子之間的相互作用和運動, 用于對材料進行的疲勞性能仿真。MD 利用計算機數值求解分子體系運動方程的方法,模擬研究分子體系的結構與性質。該技術不僅可以得到原子的運動軌跡, 還可以觀察到原子運動過程中各種微觀細節。分子動力學模擬材料分子之間的相互作用, 考慮結構中彈性變形和非彈性變形的過程。這些方法適用于預測微小尺度下材料的疲勞行為。通過對模擬軌跡進行聚簇等分析, 可獲得分子間各狀態相對穩定構型, 并通過分析分子間相互作用模式和相互作用能等來鑒定分子間作用機理。 多晶銅在不同疲勞狀態下的變形機制及位錯密度變化不同, SAINATH G 等采用分子動力學方法研究了晶粒尺寸為5.4 nm 的多晶銅的疲勞變形行為。圖15 為分子動力學模擬結果, 表明了在循環載荷作用下的變形行為主要是包裹層錯的部分位錯滑移。在較高的循環次數下, 出現晶界遷移導致大晶粒粗化而犧牲小晶粒。其中紅色原子代表晶界、 位錯核和表面原子。藍色原子代表完美FCC原子, 青色原子代表HCP原子。 圖15 納米多晶Cu在3%應變下第1次(a)、 第5次(b) 和第10次(c) 循環塑性變形 綜上所述, 高周疲勞壽命的預測可以通過經驗法、 確定性分析法、 累計損傷法和數值模擬法等多種方法來實現。需要注意的是, 高周疲勞性能預測是一個復雜的問題, 涉及到材料的微觀結構、 金屬內部缺陷、 應力分布和載荷歷史等多個因素的相互作用。因此, 選擇合適的預測方法需要考慮材料特性、 可用數據和預測準確度。結合多個方法和綜合分析, 可以提供更準確的高周疲勞性能預測結果。 4.總結與展望 通過對金屬材料高周疲勞性能及模擬的研究進行綜合梳理, 對材料表征方法、 仿真模型和實驗技術的最新發展進行了總結, 了解到金屬高周疲勞性能及模擬的研究已經取得了一系列重要進展。這些研究不僅揭示了金屬材料微觀結構與高周疲勞性能之間的關系, 還開發了精確可靠的仿真模型, 能夠預測金屬材料在高周循環載荷下的疲勞行為。 然而金屬材料高周疲勞性能及模擬研究仍存在一些問題和挑戰, 需要建立全面和準確的材料性能數據庫。此外, 現有的模擬方法和實驗技術在復雜應力狀態下的適用性和可靠性仍有待改進。未來的研究方向將集中在以下幾個方面, 以進一步推動金屬高周疲勞性能及模擬的發展。 (1) 改進材料表征技術, 尤其是在微觀結構表征方面, 包括應用先進的顯微觀察技術和原位測試方法, 以更深入地理解微觀結構與高周疲勞性能之間的關系。 (2) 發展更準確和可靠的仿真模型, 尤其是考慮復雜應力狀態下的行為。這包括更準確地建模材料的塑性變形、 損傷積累和疲勞斷裂過程, 以預測材料在高周循環載荷下的壽命。 (3) 建立全面和準確的材料性能數據庫是關鍵。這需要加強數據收集和共享, 并建立統一的評估方法和標準, 以便研究人員可以更好地利用這些數據進行高周疲勞性能的預測和比較分析。 (4) 針對金屬材料在實際工程中的應用需求,需要將高周疲勞性能及模擬研究結果應用于工程實踐。這涉及到開發適用的損傷評估和壽命預測方法,以指導結構設計和優化。 (5) 通過進一步研究和改進, 金屬高周疲勞性能及模擬的應用將為工程領域提供更加準確可靠的材料性能信息, 從而提高工程結構的可靠性和壽命,推動技術的發展與創新。
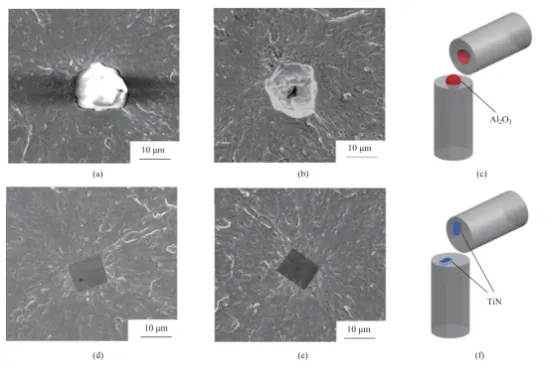
(a)Al2O3夾雜物圖 (b)Al2O3夾雜物剝離圖 (c) 含Al2O3夾雜物的疲勞斷裂示意圖(d) TiN夾雜物圖(e) TiN 夾雜物剝離圖(f) 含TiN夾雜物的疲勞斷裂示意圖
(a)104次后晶界處產生的位錯 (b) 104次后位錯滑動 (c) 104次后位錯堆積(d) 106次后晶粒內部的位錯胞 (e) 106次后位錯胞放大視圖 (f) 106次后位錯纏結
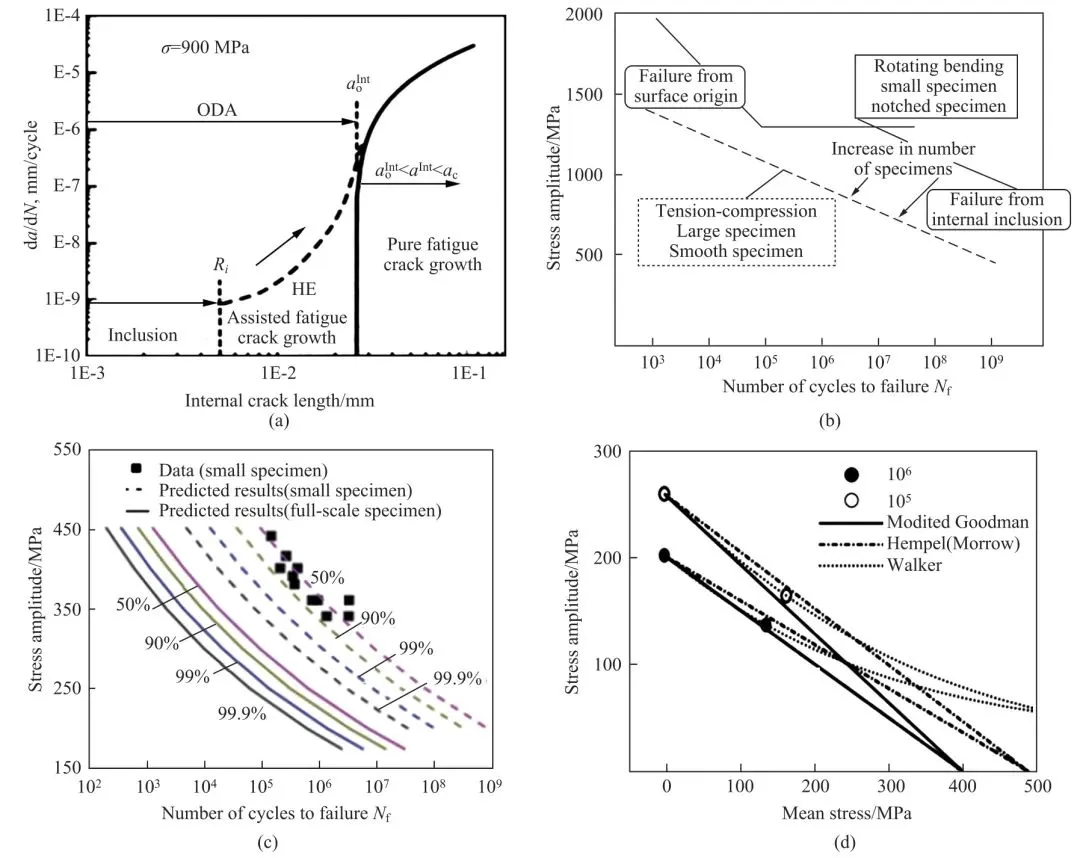
(a) 疲勞裂紋擴展速率與裂紋長度關系 (b) 隨載荷類型及試樣尺寸變化的S-N 曲線(c) 小試樣數據預測的鐵路軸P-S-N曲線 (d) 球墨鑄鐵的P-S-N曲線
免責聲明:本網站所轉載的文字、圖片與視頻資料版權歸原創作者所有,如果涉及侵權,請第一時間聯系本網刪除。

官方微信
《腐蝕與防護網電子期刊》征訂啟事
- 投稿聯系:編輯部
- 電話:010-62316606
- 郵箱:fsfhzy666@163.com
- 腐蝕與防護網官方QQ群:140808414