唐云濤 劉子蓮 左新浪 工業和信息化部電子第五研究所

目前，針對碳鋼在潮濕環境中的可靠性分析中，主要通過結構件腐蝕深度模型來計算結構件在服役期間內的厚度均值和方差，然后根據均值和方差來判斷結構件的強度是否符合現階段的設計要求，因此合理的腐蝕模型是該方法的首要任務。碳鋼在潮濕的環境中可能會發生全面腐蝕或者局部腐蝕，現已有大量的腐蝕模型被提出。

1 全面腐蝕模型

現有的全面腐蝕模型大致可以分為兩類：經驗模型和物理模型，經驗模型主要是基于結構件在潮濕環境中的實際測量數據，然后通過實際的方法擬合出曲線，物理模型主要是基于腐蝕涉及到的物理學原理推導得出[1-2] 。

1.1經驗模型

早些年間，科學家們假定腐蝕具有恒定的腐蝕速率，不同階段的腐蝕速率不同，據此，1979 年，Southwell [3] 等提出了線性以及雙線性模型，通過目前學者的腐蝕研究數據可知，線性模型不能準確的解釋結構件在實際服役環境中的發生的腐蝕行為，更不能預測后期腐蝕深度。1998 年 Paik 等[1-2]采用統計學方法將腐蝕模型劃分為兩個階段：腐蝕防護系統有效階段和腐蝕發生階段，為了便于分析假定腐蝕發生在腐蝕防護系統失效以后，同時 Paik 等假定耐蝕涂層壽命服從正態分布，假定耐蝕涂層失效后的腐蝕速率與腐蝕時間呈現冪函數關系，Paik 的腐蝕模型如圖 1 所示，圖中 t τ 為腐蝕深度，T 為結構件的服役時間，Tc 為耐蝕涂層的壽命，Tt 為過渡時間，C 1 和 C 2 為系數，該腐蝕模型冪指數的大小可以模擬出不同的腐蝕過程，當冪指數大于 1 時，腐蝕模型為 C，腐蝕速度不斷加快，可以模擬腐蝕產物不斷被清理的過程；當冪指數等于 1 時，腐蝕模型為 B，即為恒定腐蝕速率；當冪指數小于 1 時，腐蝕模型為 A，表明腐蝕速率不斷降低，可以模擬腐蝕產物不斷堆積的過程。

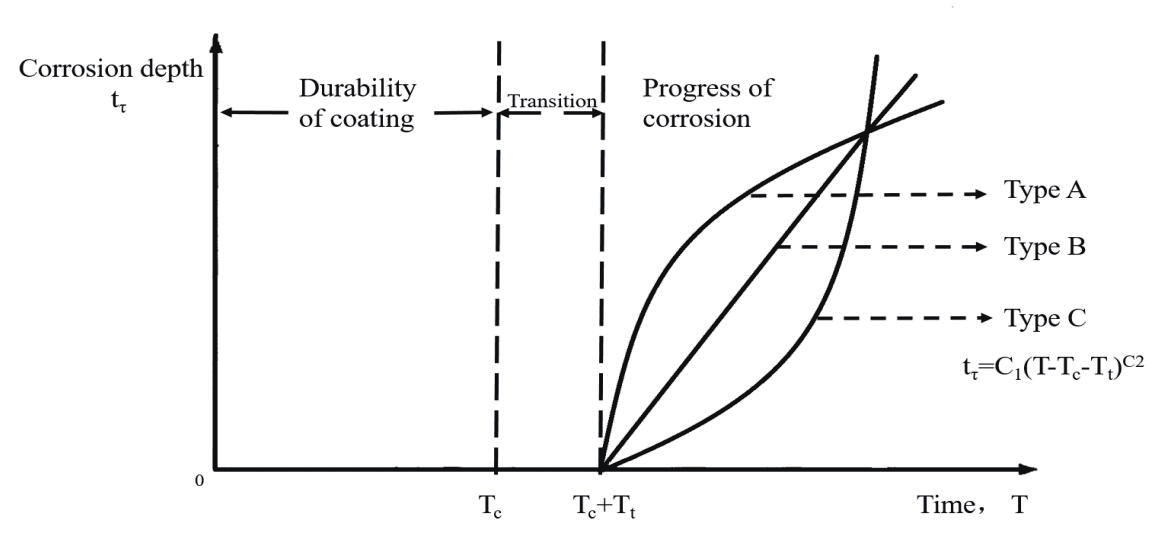
圖1 Paik腐蝕模型

1999 年，Guedes Soares 和 Garbatov [4] 提出了非線性腐蝕模型，該模型與 Paik 的模型相一致，主要描述了腐蝕過程的三個階段，分別是耐蝕涂層保護有效過程、耐蝕涂層發生破壞，腐蝕深度非線性增長過程和腐蝕產物減緩了腐蝕速率的過程。根據上述三個腐蝕階段的假定，Guedes Soares 和Garbatov 假設耐蝕涂層的壽命服從統計學上的正態分布，提出了一個腐蝕模型，該模型的形式為指數函數，并成功的運用該模型描述了貨輪側板在海洋潮濕環境下的腐蝕過程。上文中提到的指數函數腐蝕模型和冪函數腐蝕模型數學形式較為簡單，應用方便，但他們均認為腐蝕發生在耐蝕涂層失效以后，而沒有認識到腐蝕與耐蝕涂層失效是同時發生的。2003 年，秦圣平和崔維成[5]提出了可靠性分析中常用的 Weibull 函數形式的腐蝕深度概率模型，該函數不僅應用在腐蝕領域，也應用在其他模式失效的領域，具有相當廣范圍的應用性。Weibull 模型能夠同時描述結構件腐蝕過程的加速和減速階段，更符合實際應用中的腐蝕情況。

上述的腐蝕模型雖然具有較強的應用價值，但經驗模型需要通過大量的實驗進行數據收集，并對模型進行校正，且應用模式較為單一，在同一腐蝕環境收集的數據只能應用在當前環境，無法對另一腐蝕環境進行預測。

1.2物理模型

物理模型以腐蝕過程中的熱力學、離子擴散理論等為基礎，在上世紀六十年代，Evans [6] 等認為鐵離子的遷移為腐蝕過程中的主要控制因素。九十年代左右 Chernov [7] 等認為氧在腐蝕介質中的擴散速度是腐蝕過程中的主要控制因素，同時，他們還綜合考慮了溫度，氯離子濃度等其他因素的影響。

近現代，Melchers [8] 提出了一個概念性腐蝕模型，模型示意圖如圖 2 所示，該模型也稱為“多階段現象學腐蝕模型”。該模型描述了無耐蝕涂層下碳鋼等結構件在潮濕環境中的全面腐蝕過程，該模型將腐蝕過程分為四個階段：（1）初始腐蝕階段；（2）腐蝕產物生長所導致的氧氣擴散控制階段；（3）有氧活動控制階段；（4）厭氧活動控制階段。Melchers 通過大量實驗結果表明：在初始腐蝕階段，腐蝕速率保持穩定，在氧氣擴散控制階段，腐蝕速率隨著時間呈現出非線性變化，即在該階段剛開始時速率大，而后逐漸減小，在有氧活動和厭氧活動控制階段，腐蝕速率與腐蝕時間呈現出冪函數的變化規律，并且該階段的腐蝕狀態與腐蝕環境的氧氣擴散呈現出比例關系。“多階段現象學腐蝕模型”是近年來代表性的創作之一，他能夠簡潔明了的指出結構件在潮濕環境中的腐蝕規律，但它也具有一定的缺陷，即僅適用于沒有耐蝕涂層并且發生全面腐蝕的結構件，而且其實用性不強，因此，現階段還很難將其應用。

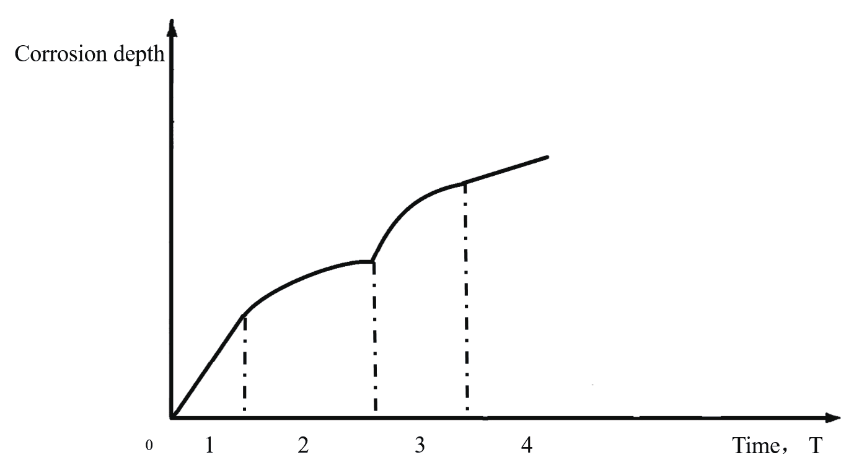
圖2 多階段現象學腐蝕模型

2 局部腐蝕模型

現階段對于局部腐蝕的研究對象集中在點蝕方面，且模型也不成熟，處于初級階段，目前科研人員認為點蝕腐蝕坑深度與腐蝕時間的關系呈現為冪函數的形式，如下式1所示。式中 d（t） 式點蝕坑的深度，t 是暴露時間，ti 是點蝕發生的時間，c1 和 c2 是待定系數。

d（t）c1（t-ti）c2，t ≥ ti （式 1）

式 1 的模型主要適用于短期腐蝕，而在長期腐蝕中的應用存在較大偏差，也有學者認為該短期腐蝕模型是由于厭氧環境引起的。

2003年，Paik等[1-2] 學者通過統計學分析后，提出了式2，并認為該模型可以用于描述結構件在潮濕環境中的局部腐蝕行為，式 2 中，Tc 是耐蝕涂層壽命，并假設其服從對數正態分布，d（t） 是腐蝕速率，為隨機變量，且服從 Weibull分布。該模型雖然在實際應用中存在一定的借鑒意義，但是無法解釋腐蝕過程的相關理論。

d（t）c1（t-Tc），t≥Tc （式2）

2005 年 Melchers [8] 將點蝕坑深度服從 Gumbel 分布，而且結合全面腐蝕模型中的多階段現象學模型建立了碳鋼在潮濕環境中的最大點蝕坑深概率模型，如圖 3 所示，該模型也稱為點蝕現象學腐蝕模型，模型一共分為 5 個階段：第 0階段用于點蝕微觀層面的描述，點蝕初始時腐蝕速率迅速增大，此時腐蝕速率主要取決于碳鋼表面是否有涂層以及腐蝕環境的惡劣程度；第 1 階段取決于活化控制的情況，腐蝕環境中的氧的擴散速率起到了關鍵作用；第 2、3 和 4 階段用于描述宏觀點蝕，第2 階段時，潮濕環境中的氧氣溶解擴散速率在腐蝕產物影響下會發生較大的變化，此時腐蝕產物起到了關鍵性作用；第 3 階段和第 4 階段表明在厭氧控制下，點蝕坑深緩慢增長。該點蝕模型具有較高的可信度，但是，它也有一定的缺陷性，比如，模型參數多，模型階段性較多，在運用的過程中較難判斷點蝕坑位于哪一階段，參數也需要大量數據推算。

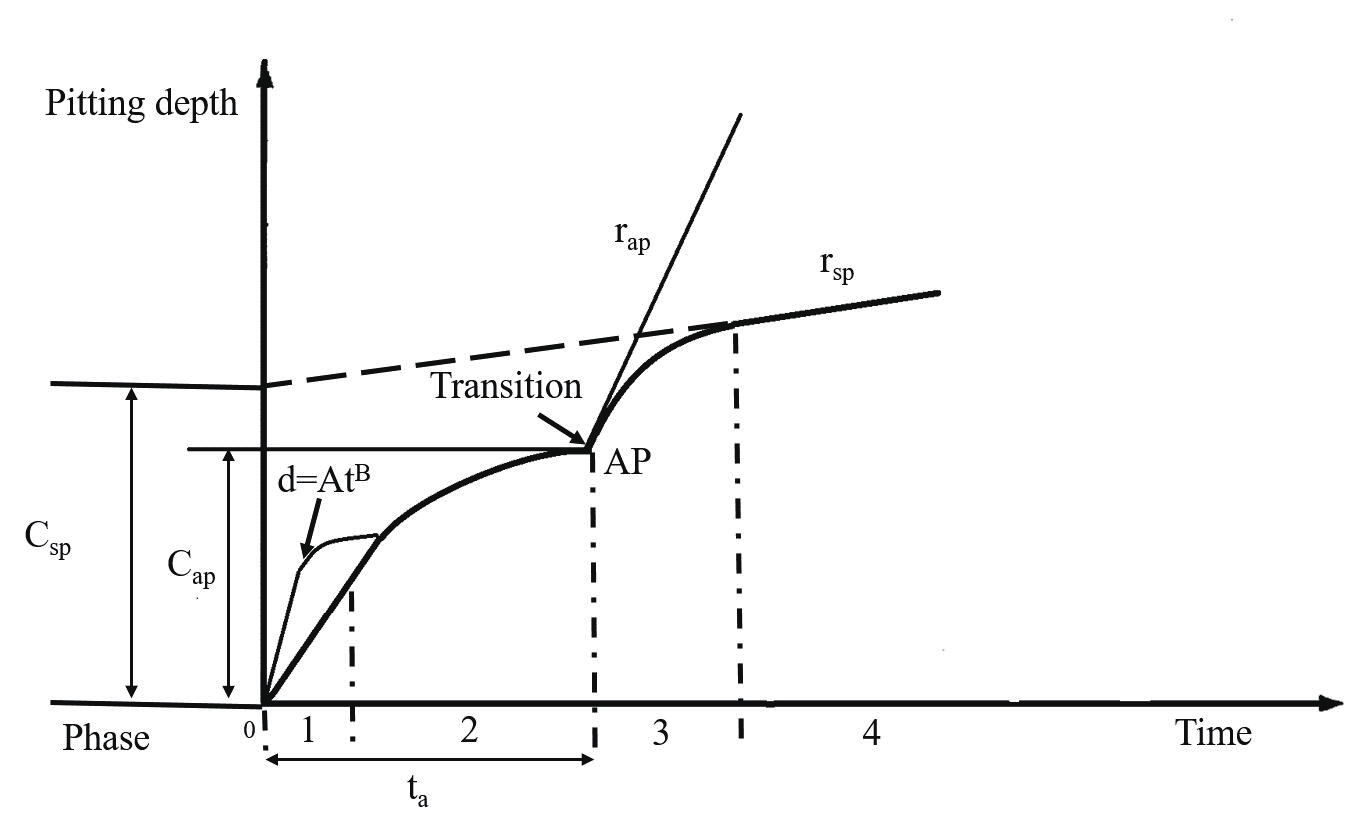
圖3 點蝕現象學腐蝕模型及參數

在全面腐蝕模型中，應用較為廣泛的屬于 Weibull 模型，在點蝕模型中，Weibull 模型也依然適用，2008 年，王燕舞[9]提出了適用 Weibull 函數來描述點蝕坑深與腐蝕時間的關系，如式 3 所示，式中，dm 是點蝕坑深度最大值，Ti 是點蝕坑發生的時間，α 和 m 是待定系數。在實際應用過程中，該模型參數為隨機變量，可以通過大量的實驗數據可以獲得參數的數值和方差。相比較于傳統的模型，該模型更為直接清楚的描述點蝕坑深隨著時間變化的規律，此外，該模型參數較少，較為容易確定。但該模型與其他的經驗模型一樣，無法對點蝕坑的微觀腐蝕機理進行研究，具有一定的不足。

d（t）dm{1-exp[-α（t-Ti ）m]}，t ≥ Tc （式 3）

4 結論

通過總結前人提出的大量腐蝕模型可知現階段腐蝕模型研究主要以全面腐蝕為主，且全面腐蝕已經積累了較多的數據，而點蝕模型由于影響因素較多，點蝕坑實測難度比全面腐蝕大，缺乏比較完整的點蝕數據庫，因此點蝕模型尚處于研究論證階段。但無論是全面腐蝕還是局部腐蝕，統計學方法均可以對其進行相關的預測，因此通過統計學對腐蝕壽命進行預測將來是重點的發展方向，但同時也需要相關科研人員完善腐蝕機理研究以便更好地應用模型。

參考文獻 ：

[1] Paik J K, Thayamballi A K. Ship-shapedoffshore installations: design, building, andoperation. New York: Cambridge University Press,2007.

[2] Paik J K, Kim D K. Advanced method for thedevelopment of an empirical model to predict time-dependent corrosion wastage. Corrosion Science,2012,63:51-58.

[3] Southwell C R, Bultman J D, Hummer CW. Estimating service life of steel in seawater.In:Schumacher M, editor. Seawater CorrosionHandbook. New Jersey: Noyes Data Corporation,1979:374-387.

[4] Soares C G. Garbatov Y. Reliability ofmaintained, corrosion protected plates subjected tonon-linear corrosion and compressive loads. MarineStructures, 1999,12（6）425-445.

[5] Qin S P, Cui W C. Effect of corrosion modelson the time-dependent reliability of steel platedelements, Marine Structures, 2003, 16（1）：15-34.

[6] Evans U R. The corrosion and oxidation ofmetals: scientific principles and practical application,London: Edward Arnold, 1960.

[7] Chernov B B, Ponomarenko S A.Physicochemical modelling of metal corrosion inseawater. Protection of Metals, 1991, 27（5）：612-615.

[8] Melchers R E. Modeling of marine immersioncorrosion for mild and low-alloy steels-part 1:phenomenological model. Corrosion, 2003,59（4）：319-334.

[9] Wang Y W. Study on the ultimate strength ofship structure considering corrosion [Dissertation].Shanghai: Shanghai Jiaotong University, 2008（ 王燕舞 . 考慮腐蝕影響船舶結構極限強度研究 [ 學位論文 ]. 上海：上海交通大學，2008）