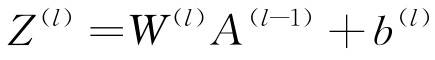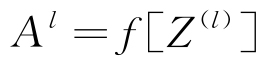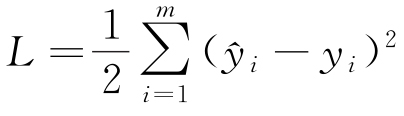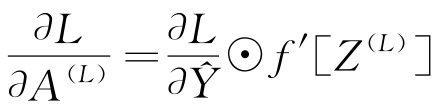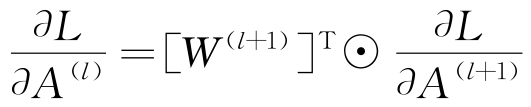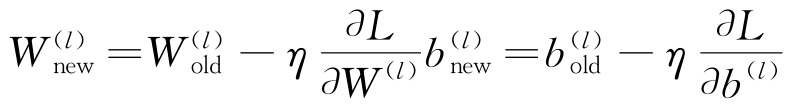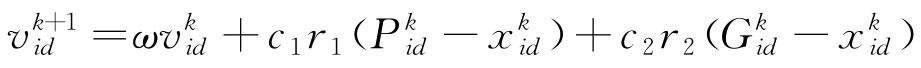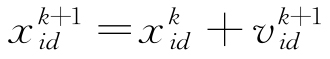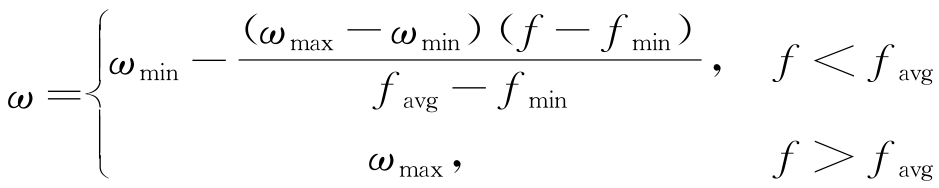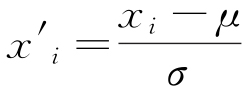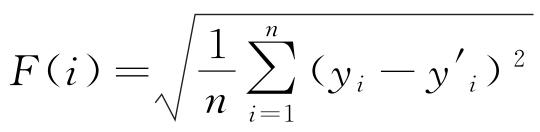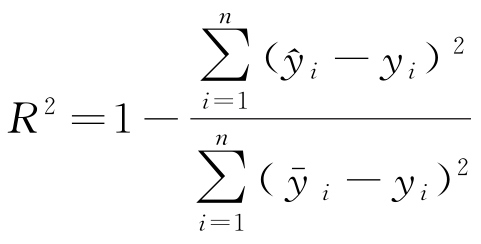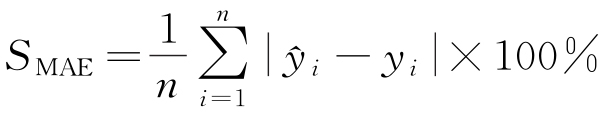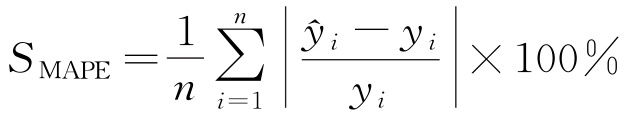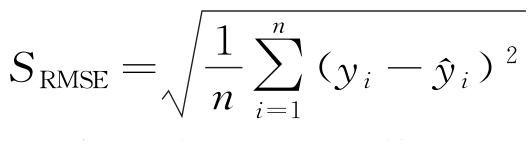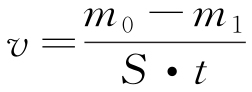鐵質材料因其固有的化學活潑性,極易發生腐蝕,尤其是在復雜的濱海環境中,受溫度、濕度、鹽度、污染物如SO2等多種因素及其耦合作用,其腐蝕問題尤為突出。腐蝕速率作為評估鐵質材料在該環境中耐久性的核心指標,其精確預測對于設計有效的防腐蝕措施和延長材料使用壽命具有不可估量的價值。因此,開展濱海環境中的鐵質材料腐蝕速率預測研究,成為提升鐵質材料防腐蝕性能和保障海洋工程安全的一項重要任務。
由于腐蝕環境的復雜性和非線性特征,傳統預測模型難以全面捕捉并準確預測金屬腐蝕速率。近年來,機器學習技術憑借其強大的數據處理和模式識別能力,在構建腐蝕預測模型方面展現出了巨大潛力。YAN等[1]提出了一種基于機器學習技術的方法,模擬了低合金鋼在海洋大氣中的腐蝕行為,評估了材料、環境因素與腐蝕速率之間的關系。姜海生等[2]采用循環神經網絡(RNN)對腐蝕探針的監測數據進行訓練,建立了管道腐蝕速率預測模型。李昊燃等[3]構建了無偏灰色模型,并通過背景值優化和數據實時更新,引入馬爾科夫模型修正預測結果,應用于油氣集輸管道腐蝕預測,顯著提升了預測精度。駱正山等[4]對傳統灰色馬爾科夫預測模型進行了優化,通過二次平滑處理和白化系數尋優,提高了埋地管道腐蝕速率預測的準確性。前述模型普遍存在對復雜環境適應性不足、參數調優困難等問題。因此,有研究引入了粒子群優化(PSO)算法,通過智能優化模型參數,提升腐蝕速率預測的準確性和穩定性。例如,印翔等[5]提出了基于PSO算法的灰色預測模型,并應用于海底管道腐蝕速率預測。蔡起衡等[6]利用PSO算法優化結合多種機器學習算法構建了Hybrid模型,然后建立了PSO-Hybrid模型,使得平均準確度和馬修斯相關系數分別提高了3.3%和8.3%。
現有研究為探明環境因素與鐵質材料腐蝕速率之間的關系提供了寶貴的參考。然而,在濱海環境中需要綜合考量溫度、濕度、氯化鈉顆粒物、其他種類污染物及其動態變化等多重復雜因素。這些因素相互作用,形成了一個高度非線性且多維度的腐蝕系統,使得腐蝕速率的預測變得尤為復雜。基于此,筆者利用自適應粒子群優化(APSO)算法對反向傳播神經網絡(BPNN)中的權重和閾值進行參數尋優,構建了一個APSO-BPNN模型,用于模擬濱海環境中鐵質材料的腐蝕速率預測。BPNN因其結構簡潔、參數靈活、訓練方法多樣和易于操作等特點,在眾多領域廣泛應用[7]。與傳統的預測方法相比,BPNN的優勢主要體現在其對非線性問題的建模具有更好的適應性和泛化能力。但是,傳統BPNN模型對初始權重和閾值的選擇高度敏感,訓練速率較慢,且容易陷入局部最優解,導致模型泛化能力受限。APSO作為一種啟發式全局優化算法,能夠通過動態調整粒子群的搜索策略來避免陷入局部最優解,增強了算法的全局搜索能力。APSO結合BPNN的非線性映射能力,不僅能夠提高神經網絡權重和結構的優化質量,還能夠提升模型對復雜濱海環境因素影響下腐蝕速率預測的精確度和魯棒性。
1. APSO-BPNN理論基礎
1.1 反向傳播神經網絡
BPNN是Rumelhart等[8]于1986年開發的一種標準的多層前饋神經網絡,其拓撲結構由輸入層、隱藏層和輸出層構成,且層間神經元全連接,層內神經元不相連[9]。該網絡通過隨機初始化連接權重和閾值,并依據訓練樣本調整這些參數,從而精確映射輸入與輸出的關系[10]。
算法具體流程如下[11]。
(1)初始化網絡參數
權重矩陣W(l)和偏置向量b(l)被隨機初始化,l表示層的索引。
(2)前向傳播
對于輸入層,直接將輸入數據X傳遞到下一層。
對于每一層l,計算加權和Z(l),見式(1)。
|
|
(1) |
應用激活函數f來獲取激活值Al,見式(2)。
|
|
(2) |
(3)輸出層計算
最后一層的激活值Al作為網絡的預測輸出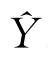 。
。
(4)損失函數計算
使用損失函數L來計算預測輸出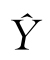 和實際輸出Y之間的差異,例如均方誤差(MSE),見式(3)。
和實際輸出Y之間的差異,例如均方誤差(MSE),見式(3)。
|
|
(3) |
式中:m是輸出的維度。
(5)反向傳播
計算輸出層的誤差梯度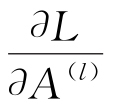 ,見式(4)。
,見式(4)。
|
|
(4) |
對于隱藏層l<L,計算誤差梯度,見式(5)。
|
|
(5) |
(6)權重和偏置更新
計算權重和偏置的梯度,并使用梯度下降法更新,見式(6)。
|
|
(6) |
式中:η是學習率。
(7)迭代訓練
重復步驟(2)至(6),直到滿足某個停止條件,如損失函數值減小到一個可接受的閾值或達到預設的迭代次數。
BPNN的學習過程實際上是信號正向傳輸和誤差反向傳播的往復循環過程,通過調整和校正連接權重和閾值來減小輸出之間的誤差,以達到收斂狀態。BPNN在非線性系統的仿真中具有良好的適用性,也適用于大量信息的并行處理[12]。然而,BPNN有一些固有的缺點,包括性能高度依賴于拓撲結構、初始連接權重和連接節點的閾值,并且在訓練過程中表現出較慢的收斂速率和較大的波動性,容易陷入局部最優解。因此,為了避免其陷入局部最優,采用一種群體智能學習算法對BPNN進行了參數的尋優改進。
1.2 自適應粒子群優化算法
PSO是一種經典的群智能優化算法,由EBERHART和KENNEDY[13]于1995年提出。它通過使用一種簡單的機制來模仿鳥類覓食中的群體行為來引導粒子在搜索空間中運動,從而尋找全局最優值[14]。PSO因其適用范圍廣、原理簡單、超參數少、收斂快、具有較好的全局尋優能力等特點[15-16],而廣泛應用于各個領域。
PSO的數學模型定義如下:設有N個粒子組成的種群,表示為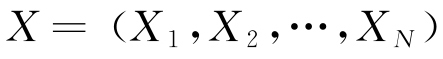 ,各粒子的位置與速度均為D維向量,其中第i個粒子的位置及飛行速度分別為
,各粒子的位置與速度均為D維向量,其中第i個粒子的位置及飛行速度分別為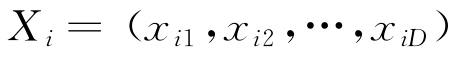 和
和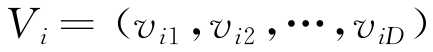 ,
, 。在算法的迭代過程中,每個粒子的速度和位置表示見式(7)~(8)。
。在算法的迭代過程中,每個粒子的速度和位置表示見式(7)~(8)。
|
|
(7) |
|
|
(8) |
式中:k為當前迭代次數;d=1, 2,…,D;ω為慣性權重,用于調節PSO的尋優能力,較大的ω值有利于全局搜索,而較小的ω值則更利于局部優化[17],通常ω∈[0,1];c1,c2為加速度常數,分別調節粒子向局部最優位置和全局最優位置的邁進步長,通常c1=c2∈[0,2];r1,r2為相互獨立的隨機數,均勻分布在[0,1]區間內,用于搜索隨機性的增加。粒子在每次迭代中通過追蹤個體最優位置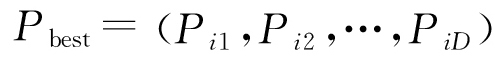 和群體最優位置
和群體最優位置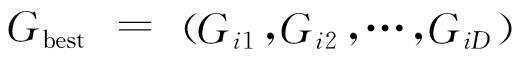 ,不斷更新自身的位置和速度,實現最優解的搜尋[18]。
,不斷更新自身的位置和速度,實現最優解的搜尋[18]。
傳統PSO的性能依賴于其參數的選取,其中慣性權重ω是關鍵參數[19],它決定粒子保持歷史速度的程度[20],從而影響算法性能。然而,由于ω的線性遞減和信息利用不全,搜索方向缺少指導,且在接近全局最優解時容易產生振蕩,這可能導致低收斂速率、局部最優陷阱和過早收斂[21]。為解決這些問題,APSO引入了基于粒子適應度和群體平均適應度的動態慣性權重調整,同時動態改變粒子的飛行時間[22]。
APSO的自適應慣量權重表示見式(9)。
|
|
(9) |
式中:f為當前粒子的函數值;favg為目標函數的平均值;fmin為全局最優值(最小值)。本文選取ωmax=1.2,ωmin=0.4。
2. APSO-BPNN模型構建
2.1 建模流程
APSO-BPNN模型使用測試集樣本進行評估,具體的建模步驟如下,流程示意詳見圖1。
(1)建立BPNN模型
選擇隱藏層節點數為7的三層網絡結構,訓練步長設為100,學習速率設為0.01,目標誤差設為0.000 1,使用trainlm函數作為訓練函數。激活函數方面,輸入層到隱藏層使用logsig函數,而隱藏層到輸出層則采用purelin函數。
(2)數據預處理
對采集到的數據(溫度、相對濕度以及SO2、NO2、O3、甲酸和NaCl顆粒物的濃度)進行Z-score歸一化處理,見式(10)。
|
|
(10) |
式中:xi為原始數據;σ為樣本數據的標準差;μ為樣本數據的均值;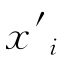 為歸一化處理后的數據。
為歸一化處理后的數據。
(3)APSO算法參數設置
設置種群規模為30,進化次數定為300。粒子速度的變化范圍限定在[-1,1],搜索空間為[-100,100]。慣性權重ω的范圍設為[0.4,1.2],加速度常數c1=1.9,c2=1.7。
選擇種群規模為30可以在計算成本和搜索多樣性之間取得平衡,避免陷入局部最優。進化次數設為300次,保證了充分的迭代次數以實現良好的收斂性。粒子速度范圍限定在[-1,1],通過控制步長精確定位最優解。搜索空間設為[-100,100],確保涵蓋所有潛在的解區域。慣性權重范圍[0.4,1.2]實現了全局探索與局部開發的平衡。加速常數設置為c1=1.9和c2=1.7,在個體和群體影響力之間保持合理的比例,使粒子既能充分探索搜索空間,又能有效收斂到最優解。
(4)適應度函數定義
定義適應度函數F(i)為均方根誤差(RMSE),用于衡量模型預測結果與實際值之間的偏差,見式(11)。
|
|
(11) |
式中:yi為真實值; 為模型預測的輸出值;為輸出節點的數量。
為模型預測的輸出值;為輸出節點的數量。
(5)模型優化
使用APSO算法迭代更新粒子的速度和位置,從而優化BPNN的權重和閾值。優化過程遵循以下步驟:①更新粒子速度和位置;②計算適應度函數值;③更新粒子個體最優位置和全局最優位置;④調整慣性權重以平衡全局搜索和局部搜索。
2.2 模型評價指標
為驗證APSO-BPNN模型的有效性,選用以下評價指標來評估模型的預測性能:決定系數(R2)、平均絕對誤差(MAE)、平均絕對百分比誤差(MAPE)和均方根誤差(RMSE),具體的計算公式見式(12)~(15)。
|
|
(12) |
|
|
(13) |
|
|
(14) |
|
|
(15) |
式中:n為測試集樣本量;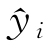 為模型預測值;
為模型預測值;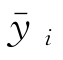 為真實值的平均值;SMAE為平均絕對誤差;SMAPE為平均絕對百分比誤差;SRMSE為均方根誤差。
為真實值的平均值;SMAE為平均絕對誤差;SMAPE為平均絕對百分比誤差;SRMSE為均方根誤差。
3. 結果與討論
3.1 暴露試驗結果
濱海區域以其獨特的地理位置,常伴隨著復雜多變的氣候條件及高濃度的海洋性污染物。針對濱海環境特點選取了溫度、相對濕度、NaCl質量濃度、SO2質量濃度、NO2質量濃度、O3質量濃度以及甲酸質量濃度七個核心環境因素,以灰口鑄鐵作為試驗材料。經過打磨、清洗、干燥和稱量處理后,將試樣置于不同環境條件下暴露1 a。根據國家標準GB/T 16545-2015《金屬和合金的腐蝕腐蝕試樣上腐蝕產物的清除》,對暴露后的試樣表面進行化學和物理清洗,以徹底去除腐蝕產物,然后進行干燥和稱量。
采用失重法計算試樣的腐蝕速率,具體的計算公式見式(16)
|
|
(16) |
式中:m0為試樣暴露前的質量,g;m1為去除腐蝕產物后試樣的質量,g;S為試樣暴露面積,m2;t為試樣暴露時間,a;v為試樣的平均腐蝕速率,g/(m2·a)。表1列出了試樣暴露的環境因素參數和腐蝕速率。
| 試樣編號 | ρ(NaCl)/(μg·cm-2) | T/℃ | 相對濕度RH/% | ρ(SO2)/(μg·L-1) | ρ(NO2)/(μg·L-1) | ρ(O3)/(μg·L-1) | ρ(HCOOH)/(μg·L-1) | v/(g·m-2·a-1) |
|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 20 | 40 | 1 | 5 | 1 | 10 | 13.2 |
| 2 | 10 | 20 | 40 | 5 | 10 | 25 | 50 | 13.0 |
| 3 | 1 | 20 | 60 | 10 | 20 | 5 | 50 | 8.6 |
| 4 | 30 | 20 | 60 | 20 | 30 | 10 | 10 | 42.0 |
| 5 | 30 | 20 | 70 | 5 | 20 | 1 | 300 | 58.0 |
| 6 | 5 | 20 | 90 | 10 | 10 | 10 | 300 | 32.0 |
| 7 | 10 | 20 | 90 | 20 | 5 | 5 | 100 | 65.5 |
| 8 | 5 | 25 | 40 | 10 | 20 | 25 | 100 | 4.0 |
| 9 | 10 | 25 | 40 | 20 | 30 | 1 | 300 | 9.0 |
| 10 | 1 | 25 | 60 | 1 | 5 | 10 | 300 | 8.0 |
| 11 | 30 | 25 | 60 | 5 | 10 | 5 | 100 | 56.0 |
| 12 | 1 | 25 | 70 | 10 | 10 | 1 | 10 | 26.5 |
| 13 | 5 | 25 | 90 | 1 | 30 | 5 | 50 | 36.0 |
| 14 | 10 | 25 | 90 | 5 | 20 | 10 | 10 | 36.0 |
| 15 | 30 | 30 | 40 | 10 | 5 | 5 | 300 | 13.0 |
| 16 | 1 | 30 | 40 | 20 | 10 | 10 | 100 | 8.0 |
| 17 | 10 | 30 | 60 | 1 | 20 | 1 | 100 | 30.2 |
| 18 | 5 | 30 | 60 | 5 | 30 | 25 | 300 | 7.0 |
| 19 | 10 | 30 | 70 | 10 | 30 | 10 | 50 | 38.0 |
| 20 | 5 | 30 | 70 | 20 | 20 | 5 | 10 | 24.0 |
| 21 | 30 | 30 | 90 | 1 | 10 | 25 | 10 | 105.0 |
| 22 | 1 | 30 | 90 | 5 | 5 | 1 | 50 | 52.3 |
| 23 | 30 | 35 | 40 | 1 | 20 | 10 | 50 | 16.0 |
| 24 | 1 | 35 | 40 | 5 | 30 | 5 | 10 | 8.0 |
| 25 | 10 | 35 | 60 | 10 | 5 | 25 | 10 | 15.0 |
| 26 | 5 | 35 | 60 | 20 | 10 | 1 | 50 | 16.0 |
| 27 | 10 | 35 | 70 | 1 | 10 | 5 | 300 | 25.0 |
| 28 | 5 | 35 | 70 | 5 | 5 | 10 | 100 | 19.6 |
| 29 | 30 | 35 | 90 | 10 | 30 | 1 | 100 | 109.0 |
| 30 | 1 | 35 | 90 | 20 | 20 | 25 | 300 | 11.0 |
3.2 APSO-BPNN模型效果評估
選取溫度、相對濕度RH、NaCl質量濃度、SO2質量濃度、NO2質量濃度、HCOOH質量濃度、O3質量濃度作為模型的輸入神經元,試驗腐蝕速率作為輸出神經元。
(1)傳統BPNN模型
為了深入探究優化模型的效果,本文構建并訓練了一個傳統的BPNN模型,其參數配置與優化后的APSO-BPNN模型保持一致。BPNN模型的訓練與預測效果見圖2,其中測試集的決定系數R2達到0.801 7,表現出良好的相關性。然而,在評價指標方面,MAE為16.39, MAPE為36.01%, RMSE為20.41,表明模型穩定性有待提高。在對測試集進行預測時,最高相對誤差接近60%,這進一步表明該模型對于濱海復雜環境中鐵質材料的腐蝕速率預測具有較高的不穩定性。鑒于此,引入APSO算法對BPNN模型的參數進行精細化調整,以提升模型的預測精度。
(2)APSO-BPNN模型
如圖3所示,隨著迭代次數的不斷增加,APSO-BPNN模型的適應度呈現出逐步下降的趨勢,這得益于APSO算法在迭代過程中多次成功跳出局部最優解的機制,從而確保了全局搜索的有效性。在迭代次數達到236次時,模型成功獲得了全局最優解,此時適應度達到了最小值0.005 6。在滿足粒子群迭代終止條件后,APSO搜索確定了最終的慣性權重ω為0.719 5。
將經過APSO算法優化得到的最優權重和閾值引入BPNN模型后,APSO-BPNN模型的訓練效果如圖4(a)所示,模型訓練得到的預測值與真實值高度重合,這充分說明模型訓練的高擬合程度。進一步觀察圖4(a)可以發現,訓練集樣本的預測值與實際值之間的相對誤差均保持在25%以內,且誤差波動較小,這充分說明了該模型在訓練集上的預測精度較高。如圖4(c)所示,訓練集決定系數R2高達0.991 3,這進一步印證了預測結果的精確性。
為了驗證經訓練集訓練的APSO-BPNN模型的精確度,將測試集數據作為輸入神經元進行預測,結果如圖4(b)所示。可見,APSO-BPNN模型對測試集樣本的預測值與真實值之間的相對誤差保持在40%以內,且最小相對誤差僅為6.9%,誤差波動范圍較小。在評價指標方面,MAE為11.55, MAPE為22.26%, RMSE為14.43,這表明經過訓練集訓練的APSO-BPNN模型對未知樣本腐蝕速率的預測效果較好,相較于傳統BPNN模型展現出較強的泛化能力。如圖4(d)所示,決定系數R2達到0.925 8,這進一步證實了在訓練小樣本數據的情況下,APSO-BPNN模型仍具有一定的預測精度和良好的預測準確性。
綜上所述,相較于傳統BPNN模型,APSO-BPNN模型展現出了更佳的泛化能力與預測精度,且穩定性更高。在應對較小數據量的腐蝕預測任務時,該模型的預測精度較高,這對于鐵質材料的腐蝕速率預測具有重要的實踐意義。
4. 結論
為深入探究濱海環境中鐵質材料的腐蝕行為,本文選取了溫度T、相對濕度RH、NaCl質量濃度、SO2質量濃度、NO2質量濃度、甲酸質量濃度以及O3質量濃度等環境因素,對濱海環境鐵質材料腐蝕的行為進行研究。采用失重法計算了鐵質材料在多因素環境中暴露1 a的腐蝕速率,并應用機器學習技術對暴露數據進行建模,構建了腐蝕速率預測模型。
對于鐵質材料在多因素環境中暴露1 a的腐蝕速率預測,傳統BPNN模型的預測效果穩定性不足,其最高相對誤差接近60%,決定系數R2僅為0.801 7,預測精度較弱。相比之下,APSO-BPNN模型展現出更佳的泛化能力與預測精度。在迭代尋優過程中,該模型成功多次跳出局部最優,最終在進化代數達到236次時穩定收斂,并確定了最終的慣性權重ω為0.719 5。訓練集的決定系數R2高達0.925 8,且相對誤差嚴格控制在25%以內;測試集的決定系數R2同樣維持在0.925 8的高水平,相對誤差不超過40%。
免責聲明:本網站所轉載的文字、圖片與視頻資料版權歸原創作者所有,如果涉及侵權,請第一時間聯系本網刪除。

官方微信
《腐蝕與防護網電子期刊》征訂啟事
- 投稿聯系:編輯部
- 電話:010-62316606
- 郵箱:fsfhzy666@163.com
- 腐蝕與防護網官方QQ群:140808414