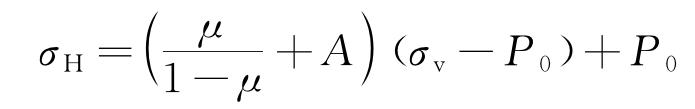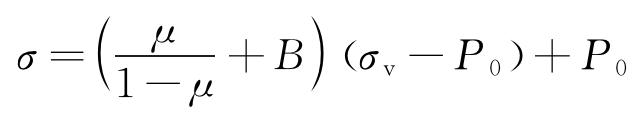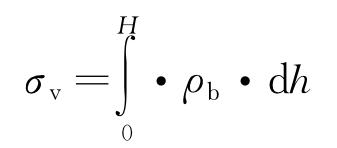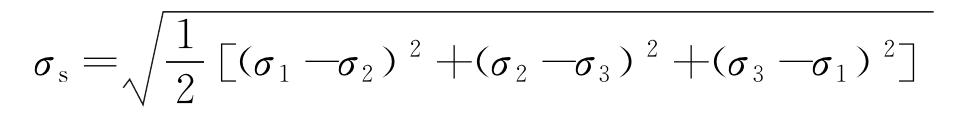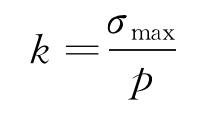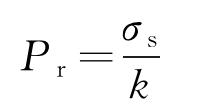隨著深井、超深井油氣資源的開采,套管面臨的腐蝕問題日益嚴重[1-2]。在復雜的工作環境中,套管既有來自地層流體壓力和地應力的機械擠壓作用,也有來自含腐蝕介質油氣對套管的化學作用[3-6]。套管腐蝕會直接影響井筒的完整性和油田企業的安全生產[7-8]。因此,對腐蝕套管進行應力和剩余強度分析是尤為重要的。 

在套管腐蝕研究領域,國內外學者主要以電化學、彈塑性力學、斷裂力學等為理論基礎[9],研究套管的腐蝕機理、剩余強度以及腐蝕速率等,并推出了一系列評估規范和方法。祝效華等[10]通過對不同形貌腐蝕缺陷進行規則化處理,研究了腐蝕缺陷類型對套管抗擠壓強度的影響。ZHANG等[11]建立了復合模態下套管磨損形態和剩余強度的預測模型,揭示了各種因素對套管強度的影響。NARHI等[12]采用熱-機械井模擬器和有限元模型分析了油井套管的嚴重腐蝕問題,評估了油井的結構完整性。MOHD等[13]利用有限元模型,分析了內壓和彎矩共同作用對套管剩余強度的影響規律。車爭安等[14]通過建立腐蝕孔應力集中系數的數學模型和剩余強度計算公式,研究了應力集中對套管強度的影響。NABIPOUR等[15]通過有限元方法模擬了井下環境,研究了內壓、水平應力差和套管偏心對套管穩定性的影響。張智等[16]通過建立腐蝕套管強度計算模型,研究了溫度、內壓、腐蝕深度、直徑因素對套管等效應力和剩余強度的影響規律。上述研究表明,應力與腐蝕的協同作用會加劇套管的腐蝕,造成套管材料提前失效。 

針對上述問題,筆者以焦頁4HF井中139.7 mm直徑、N80鋼級的套管為例,在現有理論研究基礎上,針對套管腐蝕后腐蝕缺陷形狀復雜多變的特點,選擇三類常見腐蝕缺陷形狀（凹槽形、圓球形和半圓柱形）[17],分別建立“套管-水泥環-地層”三維模型。采用有限元方法,研究了腐蝕缺陷幾何形狀和腐蝕影響因素對套管腐蝕區域應力分布情況、Von Mises等效應力和剩余強度的影響,從而得出對套管性能影響最大的腐蝕缺陷形狀,在此基礎上,同時考慮了溫度、內外壓差等因素,對含圓球形腐蝕缺陷組合體進行穩態熱-結構耦合分析。以期為含腐蝕缺陷套管的安全評價和井筒完整性評估提供技術支持。 

1.   不同腐蝕缺陷形狀套管的有限元模型

鉆井過程中,套管的力學性能受溫度、壓力、地應力、腐蝕性介質等因素的影響。考慮到套管各方面存在性能差異,在采用有限元軟件進行模擬時,不能完全模擬油套管的受力情況。為了便于建立三維模型,對“套管-水泥環-地層”模型進行如下基本假設[18-19]： 

（1）系統所有材料都是均勻的、連續的,且都為彈性體； 

（2）套管、水泥環、地層三者之間的接觸部位膠結良好、無滑動,水泥環和井壁圍巖均為均勻且各向同性體； 

（3）套管、水泥環、地層為同心圓柱； 

（4）水泥環中沒有初始應力； 

（5）系統受力是平面應變。 

1.1   模型建立

根據巖石力學和彈塑性力學理論,以套管-水泥-地層系統為研究對象,具體參數如表1所示。考慮實際油氣井狀況,為減少有限元模型的運算量,選取部分長度進行研究,取地層的外徑為1 200 mm,水泥環的外徑為215.9 mm,根據圣維南原理[20],系統整體長度取4 000 mm,以更好地消除邊界效應的影響。 

1.2   網格劃分

根據建立的“套管-水泥環-地層”三維有限元模型,采用由外向內逐級細化分段的方法掃描劃分網格,對套管局部腐蝕區域采用網格加密處理,見圖1。 

圖  1  含不同形狀腐蝕缺陷套管的有限元模型及網格劃分

Figure  1.  Finite element model and mesh division of casing with corrosion defects of groove shape (a), spherical shape (b) and semi-cylindrical shape (c)

 

1.3   載荷的邊界條件

垂直井眼周圍地層巖石受力主要包括上覆巖層壓力、巖石內孔隙流體的壓力及水平地應力。油氣井生產時,套管受力情況復雜,不僅受到內部流體壓力、軸向載荷、摩擦載荷、屈曲載荷,還受到來自地層的非均勻地層應力等。此外,整個系統還受到溫度載荷的作用[21],如圖2所示。圖2中,σv為上覆巖層壓力；σH為水平最大主應力；σ為水平最小主應力；P0為巖石孔隙流體壓力。 

圖  2  井眼周圍巖石受力示意

Figure  2.  Schematic of rock force around the wellbore

 

上覆巖層壓力σv來源于上部巖石的重力,它和巖石內孔隙流體壓力的差（σv-P0）為有效上覆巖層壓力,水平地應力σH及σ來自垂直方向上的有效上覆巖層壓力和地質構造力。地層水平地應力可以描述為[22]： 

式中：μ為地層彈性模量；A,B為構造應力系數；ρb為地層密度。 

本模型忽略和簡化了影響較小的載荷,套管僅受內壓、外壓和溫度作用。為了簡化不均勻的地層壓力,將最大和最小水平應力簡化為均勻圍壓,附加在地層周圍,模型簡化受力分析如圖3所示。“套管-水泥-地層”采用底端固定約束。 

圖  3  模型受力分析示意

Figure  3.  Schematic of model force analysis

 

1.4   套管腐蝕后剩余強度計算準則

當材料局部腐蝕區域任意一點的等效應力達到材料的屈服強度時,即發生失效。依據第四強度理論,將等效應力屈服準則作為套管失效的判定準則,Von Mises應力可表述為 

式中：σs為屈服應力；σ1、σ2、σ3分別為x、y、z方向上的主應力。 

套管在內外壓的作用下,在彈性和小變形范圍內,其最大等效應力σmax和所受內壓或外壓之比是一個常數k。 

式中：σmax為套管最大Von Mises應力；p為套管所受內壓或外壓。 

當壓力作用在套管上使其應力達到屈服強度時,將會產生塑性變形,套管極易發生變形導致損壞,根據拉梅公式,推導出套管的剩余強度公式。 

式中：Pr為套管剩余強度,MPa;σs為套管的屈服強度,MPa。 

1.5   仿真模型驗證

為了驗證所建模型的合理性和可行性,計算了有限元數值解和API標準抗擠強度（API Bul5C2）的相對誤差,并與相關文獻中的數據結果進行對比[10]。分別選取相同尺寸不同鋼級的套管作為研究對象,設置與文獻中相同的初始條件,求解不同鋼級套管的抗擠強度,得到不同鋼級套管的相對誤差,并與文獻結果進行對比,如圖4所示。本模型相對誤差為1.3%~6.6%,比文獻結果誤差更小,符合工程計算要求。 

圖  4  模擬結果與文獻結果對比

Figure  4.  Comparison of simulation results and literature results

 

2.   實例分析

選取焦頁4HF井地下3 500 m處的“套管-水泥環-地層”組合體為研究對象進行分析。研究凹槽形腐蝕坑、圓球形腐蝕坑、圓柱形腐蝕坑三種腐蝕缺陷對套管應力和剩余強度的影響。套管材料為N80鋼級,尺寸為139.7 mm×10.54 mm,彈性模量210 GPa,泊松比0.3,屈服強度552 MPa,抗拉強度689 MPa。 

2.1   凹槽形局部腐蝕坑對套管損傷分析

腐蝕對套管強度的影響主要是由于腐蝕區域邊緣處產生了應力集中,改變了套管在腐蝕區域邊緣處的應力分布和整體強度。影響套管強度的主要因素有腐蝕長度、腐蝕寬度和腐蝕深度。 

2.1.1   腐蝕寬度的影響

由圖5可見：隨著腐蝕凹槽寬度的增加,套管腐蝕區域中間部位應力逐漸減小,腐蝕邊緣應力逐漸增大,最大應力發生在腐蝕區域與套管內壁相交處,且腐蝕區域應力呈對稱狀分布。 

圖  5  不同腐蝕凹槽寬度條件下的套管應力分布云圖

Figure  5.  Cloud maps of stress distribution in casing under different corrosion groove width conditions

 

由圖6可見：隨腐蝕凹槽寬度的增加,套管的等效應力呈先急劇增大后減小再趨于平緩的趨勢,套管剩余強度呈先急劇減小后增大再趨于平緩的趨勢。在腐蝕寬度為5 mm附近出現應力最大值,是因為當腐蝕凹槽寬度較小時,腐蝕區域應力集中現象明顯,套管剩余強度急劇降低。腐蝕凹槽寬度增大到10 mm后,套管等效應力和剩余強度變化較小。當腐蝕凹槽深度為4 mm時,套管極易發生失效；當腐蝕凹槽深度超過4 mm后,套管等效應力大于屈服強度,根據失效判定準則,此時套管已失效。 

圖  6  不同腐蝕凹槽寬度條件下套管的等效應力和剩余強度

Figure  6.  Equivalent stress (a) and residual strength (b) of casing under different corrosion groove width conditions

 

2.1.2   腐蝕長度的影響

由圖7可見：隨著腐蝕凹槽長度的增加,腐蝕區域中間的應力逐漸增大,沿著長度增加方向,邊緣處應力也逐漸增大,且腐蝕區域應力呈對稱分布。 

圖  7  不同腐蝕凹槽長度條件下的套管應力分布云圖

Figure  7.  Cloud maps of stress distribution in casing under different corrosion groove length conditions

 

由圖8可見：隨著腐蝕凹槽長度的增加,套管的等效應力先急劇增加后趨于平緩,剩余強度先急劇減小后趨于平緩。腐蝕凹槽長度增加,腐蝕面積增大,因此套管等效應力增大、剩余強度減小。當腐蝕深度為6 mm、長度為50 mm時,套管已達到屈服強度,極易發生失效；當腐蝕深度低于6 mm、長度小于100 mm時,套管處于安全服役狀態。 

圖  8  不同腐蝕凹槽長度條件下,套管的等效應力和剩余強度

Figure  8.  Equivalent stress (a) and residual strength (b) of casing under different corrosion groove length conditions

 

對比圖6和圖8可知,深度的變化對套管性能的影響極大,隨著腐蝕深度的增加,套管等效應力和剩余強度的變化幅度大于腐蝕寬度和長度變化引起的應力和剩余強度的變化幅度。腐蝕腐蝕凹槽長度的增加會使應力緩慢增大,而凹槽寬度的增加,則對應力變化影響較小,說明長度因素對套管性能的影響大于寬度因素。綜上所述,套管腐蝕凹槽深度因素對套管最大等效應力和套管剩余強度的影響最大,長度因素次之,寬度因素最小。 

2.2   圓球形局部腐蝕坑對套管損傷分析

圖9中腐蝕凹陷深度比定義為腐蝕深度與套管壁厚之間的比值。由圖9可見：隨著腐蝕凹陷深度比增加,腐蝕區域底部應力逐漸減小,環向應力逐漸增大,最大應力出現在腐蝕區域與套管內壁相交的位置。 

圖  9  圓球形腐蝕坑條件下,不同腐蝕凹陷深度比的套管應力分布云圖

Figure  9.  Stress distribution cloud maps of casing with different corrosion depression depth ratios under spherical corrosion pit condition

 

分析不同圓球形腐蝕半徑和不同腐蝕凹陷深度比對套管等效應力和剩余強度的影響規律,如圖10所示。 

圖  10  圓球形腐蝕坑條件下,腐蝕半徑和凹陷深度比對套管等效應力和剩余強度的影響

Figure  10.  The influence of corrosion radius (a) and depression depth ratio (b) on equivalent stress and residual strength of casing under spherical corrosion pit condition

 

由圖10可見：套管等效應力隨腐蝕凹陷深度比增加大致呈三次函數上升趨勢,套管剩余強度隨腐蝕凹陷深度比增加呈下降趨勢,當腐蝕凹陷深度比小于30%時,等效應力和剩余強度曲線斜率隨著凹陷深度比的增大逐漸減小,這是因為隨著套管腐蝕凹陷深度逐漸增大,腐蝕區域應力集中現象減弱,不同腐蝕半徑導致的套管等效應力和剩余強度變化較小。當腐蝕凹陷深度比大于30%時,隨著腐蝕凹陷深度比增大,等效應力和剩余強度曲線斜率出現明顯增大。此外,腐蝕坑半徑越大,等效應力越大,其主要原因是隨著腐蝕凹陷深度和腐蝕坑半徑增大,套管腐蝕面積增大,套管整體強度降低。當腐蝕凹陷深度比大于70%后,套管腐蝕后應力大于其屈服強度,套管易發生失效。 

2.3   半圓柱形局部腐蝕坑對套管損傷分析

由圖11可見：隨著腐蝕長度的增加,等效應力逐漸增大,且最大應力發生在腐蝕區域的底部。 

圖  11  半圓柱形腐蝕坑條件下,不同腐蝕長度套管的應力分布云圖

Figure  11.  Stress distribution cloud maps of casing with different corrosion lengths under semi cylindrical corrosion pit condition

 

由圖12可見：隨著腐蝕長度的增加,套管等效應力整體大致呈對數函數增大的趨勢,套管剩余強度大致呈對數函數遞減趨勢,當腐蝕長度為20 mm時,應力值達到了套管屈服應力極限,此時套管剩余強度為28 MPa。當腐蝕長度小于20 mm時,隨著腐蝕長度的增加,腐蝕半徑越小,套管等效應力越大,這主要是因為腐蝕半徑越小,套管應力集中現象越明顯,應力變化越大。當腐蝕長度大于20 mm后,隨著長度的增加,半徑越大,應力越大,此時應力增大的主要受腐蝕面積的影響。 

圖  12  半圓柱形腐蝕坑條件下,腐蝕半徑和長度對套管等效應力和剩余強度的影響

Figure  12.  The influence of corrosion radius (a) and length (b) on the equivalent stress and residual strength of casing under semi cylindrical corrosion pit condition

 

3.   圓球形腐蝕坑對套管損傷分析

通過對含三種幾何形狀腐蝕缺陷的套管進行有限元分析,比較得出圓球形腐蝕坑對套管性能影響最大,為了進一步分析腐蝕對套管性能的影響,對圓球形腐蝕坑進行深入研究,對含圓球形腐蝕坑“套管-水泥環-地層”組合體進行穩態熱-應力耦合分析,在上述研究基礎上考慮溫度、內外壓差等因素對套管的影響。 

前文研究表明,套管腐蝕后應力最大部位出現在腐蝕區域。為深入研究腐蝕區域應力分布情況以及腐蝕對套管的影響,對圓球形腐蝕坑區域以徑深2 mm分別選取三個平面,且第一平面為腐蝕坑與套管內壁相交平面,第二平面距第一平面2 mm,第三平面距第二平面2 mm,三個平面的應力分布如圖13所示。可以看出,三個平面內應力均呈對稱分布,第一平面、第二平面、第三平面內應力依次減小,可見,徑深越大,應力越小。 

圖  13  圓球形腐蝕坑條件下,不同平面的內應力分布圖

Figure  13.  Distribution diagram of internal stress in different planes under the condition of spherical corrosion pits

 

在不同壓差作用下套管第一平面應力分布情況如圖14（a）所示,與第一平面垂直平面即與套管圓周方向平面的平面應力分布如圖14（b）所示,可以看出,該平面內腐蝕區域底部應力最大,分析可知腐蝕后套管應力較大位置出現在沿軸向方向第一平面兩側、腐蝕區域底部,可以進一步判斷套管將沿著軸向以及腐蝕深度方向產生腐蝕延伸。 

圖  14  應力分布隨距離、內外壓差變化

Figure  14.  Variation of stress distribution with distance and pressure difference between inside and outside:（a) stress distribution diagram of the first plane of the casing;（b) phane stress distribation diagram of circuferential of the casing

 

由圖15可知：隨著腐蝕凹陷深度比和套管壓差的增大,套管等效應力先增大后減小,再逐漸增大,當腐蝕凹陷深度比為50%時出現應力突增；套管受壓差的影響較大,壓差越大,應力越大,變形量越大。 

圖  15  壓差和腐蝕凹陷深度比對套管應力和變形的影響

Figure  15.  Effects of pressure differences (a) and corrosion dent depth ratios (b) on casing stress and deformation

 

由圖16可見：隨著溫度的增加,套管應力未發生明顯變化,即溫度對套管強度影響較小；套管變形量隨溫度增大呈線性增加,套管變形量隨壓差的增大依次減小,且不同壓差下變化量并不大,可見溫度對套管變形量影響較大,壓差因素影響較小。 

圖  16  壓差和溫度對套管應力和變形量的影響

Figure  16.  Influence of pressure difference (a) and temperature (b) on casing stress and deformation

 

4.   結論

（1）本工作模型數值解與API標準解的相對誤差為1.3%~6.6%,符合實際工程計算要求。三類腐蝕坑條件下,套管腐蝕區域應力沿套管軸線方向呈對稱分布,且兩端應力最大。應力集中現象和腐蝕面積是引起套管失效的主要原因。 

（2）套管腐蝕深度對其性能影響最大,長度次之,寬度最小。當腐蝕深度小于6 mm時套管不易發生失效。對于半圓柱腐蝕坑,隨著腐蝕長度的增大,套管應力呈對數函數增大的趨勢,剩余強度呈對數函數減小的趨勢,當套管腐蝕長度為20 mm時已達到失效狀態,此時套管剩余強度為28 MPa。 

（3）圓球形腐蝕缺陷對套管損傷最大。當腐蝕凹陷深度比大于70%后,套管發生失效。溫度對套管變形量影響較大,壓差因素影響較小。