通過電化學(xué)的方法我們能讓吉布斯自由能變大于零的化學(xué)反應(yīng)發(fā)生，讓低自由能的物質(zhì)轉(zhuǎn)化為高自由能的物質(zhì)，例如CO2 轉(zhuǎn)化為CO。通過電化學(xué)反應(yīng)將CO2轉(zhuǎn)化為CO是轉(zhuǎn)化和利用CO2的重要反應(yīng)，如何提高此反應(yīng)的效率是一個非常重要的課題。

本文介紹的這篇發(fā)表在Nature上的研究工作利用尖端離子富集的原理提高了CO2 轉(zhuǎn)化為 CO 的電化學(xué)反應(yīng)速率。文章通過COMSOL進行了有限元模擬，計算了尖端的電化學(xué)反應(yīng)過程，得到了電極附近的離子分布和電極表面的電流密度，充分闡述了尖端離子富集的物理機制。（Enhanced electrocatalytic CO2 reduction via field-induced reagent concentration[J]. Nature, 2016, 537（7620）： 382.）

文章圖文導(dǎo)讀

圖1：鉀離子在電極表面吸附能夠降低CO2在金電極表面的反應(yīng)勢壘，提高化學(xué)反應(yīng)速率。

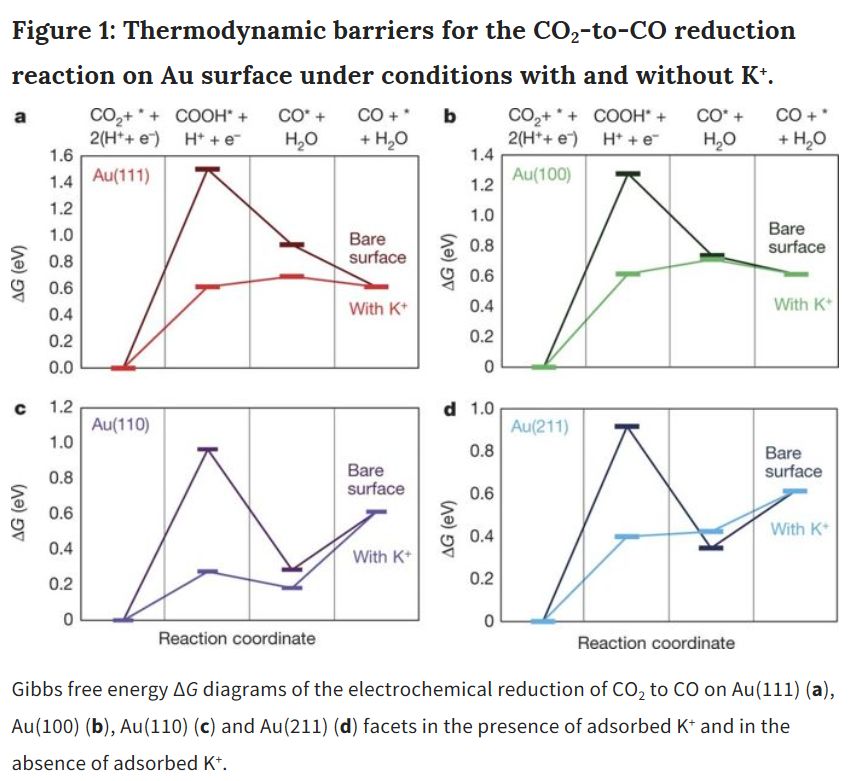
圖2：通過COMSOL 模擬計算得到電場和鉀離子在空間中的分布以及表面電流密度。CO2在陰極表面發(fā)生還原反應(yīng)，鉀離子帶正電荷能受到陰極的庫侖吸引力吸附在電極表面形成擴散雙電層。在電極尖端鉀離子濃度會更高，表面電流密度也更大。電極表面曲率越小這種富集效果越強。通過COMSOL 模擬計算得到電場和鉀離子在空間中的分布以及表面電流密度。CO2在陰極表面發(fā)生還原反應(yīng)，鉀離子帶正電荷能受到陰極的庫侖吸引力吸附在電極表面形成擴散雙電層。在電極尖端鉀離子濃度會更高，表面電流密度也更大。電極表面曲率越小這種富集效果越強。

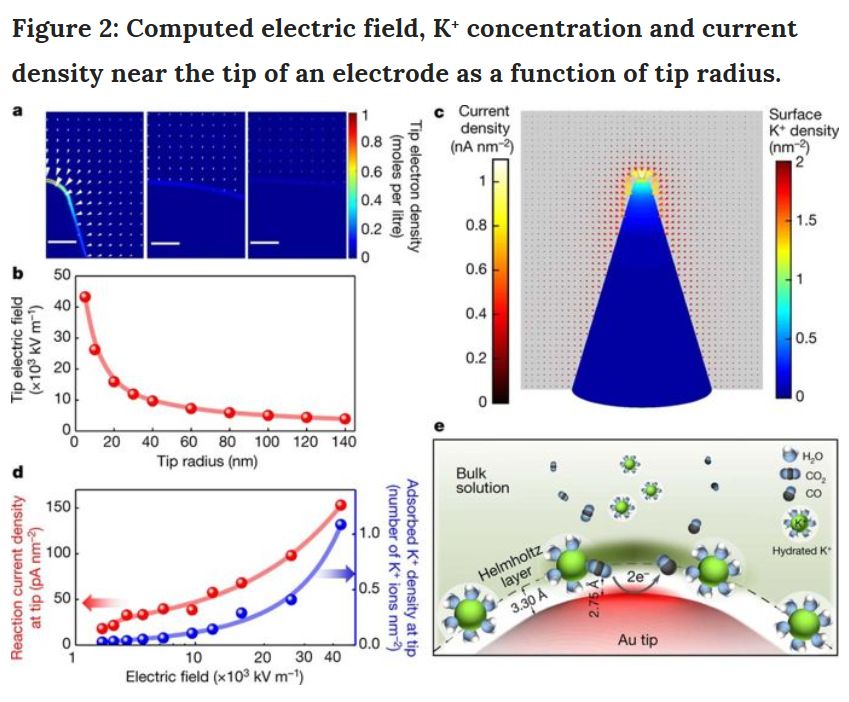
圖3：尖錐納米金、棒狀納米金和顆粒納米金的合成與表征。

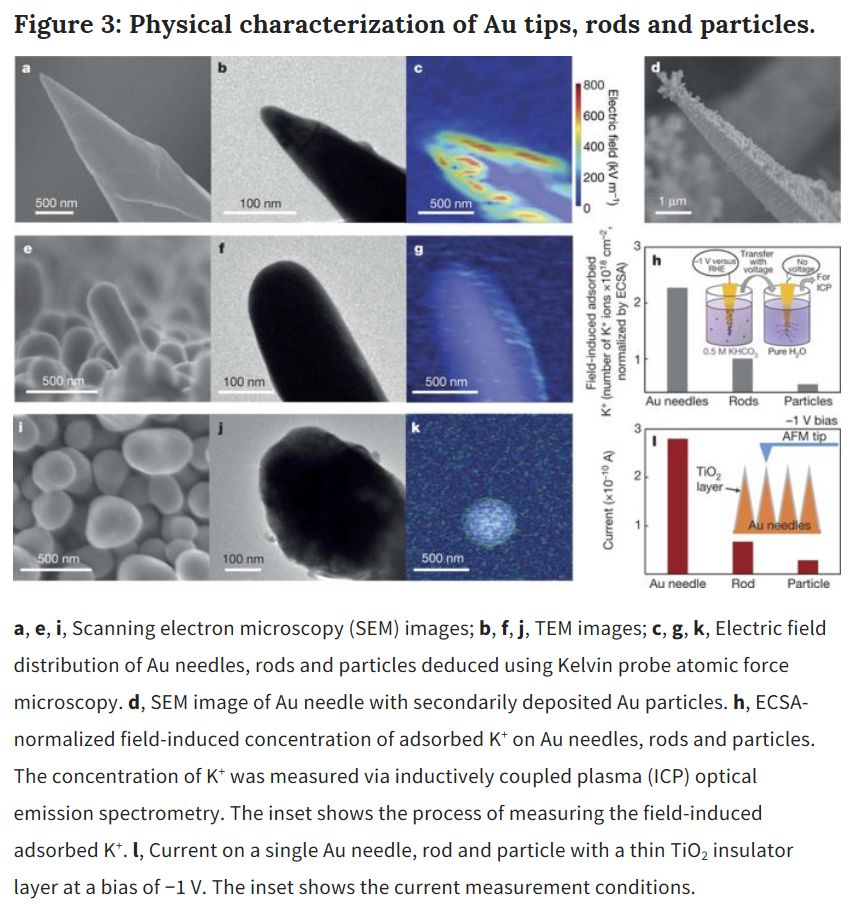
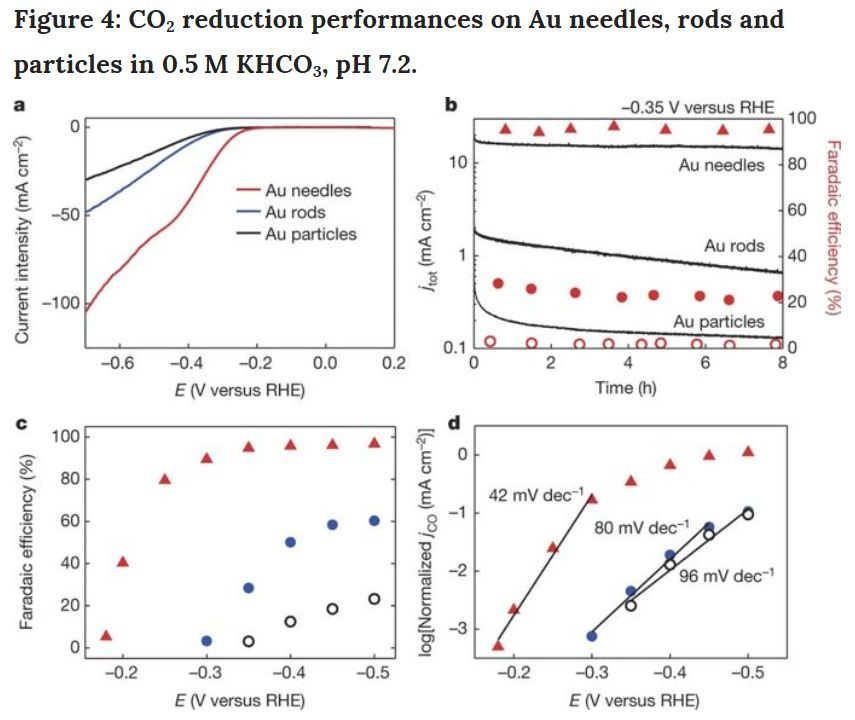
圖4：尖錐納米金、棒狀納米金和顆粒納米金在0.5M KHCO3溶液中催化CO2 還原的效果對比。尖錐納米金的催化效果要遠好于棒狀納米金和顆粒納米金，因為尖端曲率更顯鉀離子富集效果越強，降低了的CO2反應(yīng)的能壘。

文章總結(jié)：

此工作合成了尖錐狀的納米金電極，并且發(fā)現(xiàn)通過此電極能極大提高CO2的反應(yīng)速率。通過充實的理論分析，文章解釋了鉀離子在電極表面吸附能降低CO2反應(yīng)的能壘，提高反應(yīng)速率。另外模擬了尖錐狀的納米金電極表面的電化學(xué)反應(yīng)過程，通過模擬的圖像清楚的展示了尖端離子富集的機制。（Angewandte Chemie, 2018, 130（15）： 4074-4078.）

電化學(xué)模擬基本原理概述

電化學(xué)反應(yīng)的模擬會涉及到多個物理過程，包括物質(zhì)擴散，帶點離子在電場中的遷移和電極表面的化學(xué)反應(yīng)。

描述電場下的物質(zhì)擴散行為要在單純的對流擴散方程（1）的基礎(chǔ)上增加電場對帶電離子的影響，也就是Nernst-Planck方程。如果要更精確的模擬離子的分布還需要考慮帶點離子對電場的影響，這是時候需要把Nernst-Planck方程與泊松方程聯(lián)立起來求解。我們把方程（2）（3）的聯(lián)立成為Nernst-Planck-Poisson方程。通過求解Nernst-Planck-Poisson方程我們可以模擬離子在一個帶電表面附近的濃度分布。一個經(jīng)典的問題就是擴散雙電層問題。通過COMSOL模擬擴散雙電層能得到與經(jīng)典理論Gouy–Chapman–Stern 模型一致的結(jié)果。

另外對于電極表面的化學(xué)反應(yīng)通常使用Buler-Volmer方程進行計算。在給定外加電勢和電極反應(yīng)的平衡電勢的條件下，通過Buler-Volmer方程能計算表面電流密度。

除了上面提到的Nature文章，另外這里提供另一篇COMSOL電化學(xué)模擬的典型文章，Electrogenerated Chemiluminescence Imaging of Electrocatalysis at a Single Au-Pt Janus Nanoparticle （Angewandte Chemie, 2018, 130（15）： 4074-4078.）通過模擬得到了Au-Pt Janus 納米顆粒在電化學(xué)過程中顆粒周圍的物質(zhì)濃度分布。

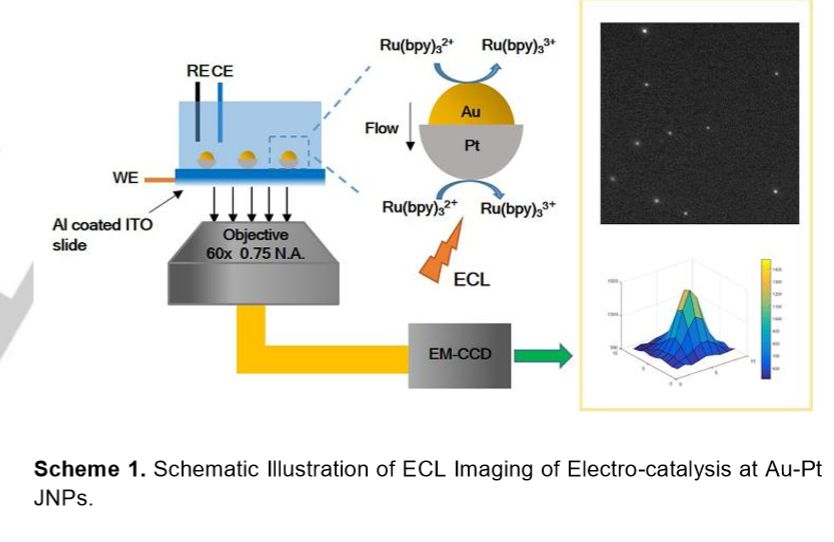
通過有限元模擬軟件COMSOL，我們可以非常方便的實現(xiàn)電化學(xué)問題的模擬。COMSOL中提供了預(yù)置的接口，可以直接基于Nernst-Planck方程Nernst-Planck-Poisson方程和Butler–Volmer方程建模。充分利用COMSOL的優(yōu)勢能夠極大的幫助我們的科研工作。

如今在高檔次文章中結(jié)合COMSOL仿真模擬來解釋科學(xué)問題，展示物理機制的方式已經(jīng)變得越來越常見。特別是對于這種機理解釋型文章，一些仿真模擬可以說是必不可少的。

COMSOL是一個多物理場仿真軟件，功能全面，覆蓋面廣泛，軟件用界面友好，如今已成為科研人員首選的模擬仿真軟件。學(xué)會使用COMSOL也是一個非常有用的科研技能。