材料的強度與破壞理論是研究材料在各種應力下的屈服或破壞的規律，本期為大家介紹那些經典的斷裂準則。

巖石開裂

最大正應力準則，也稱為第一強度理論或最大拉應力理論。

400多年以前，伽利略（Galileo: 1564-1642）在研究磚、鑄鐵和石頭的拉伸斷裂時，發現當施加應力達到一臨界值時材料發生斷裂，于是就產生了第一強度理論。

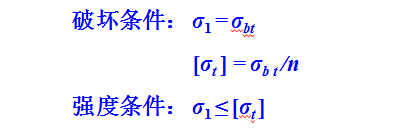
第一強度理論認為材料發生斷裂是由最大拉應力引起，即最大拉應力達到某一極限值時材料發生斷裂。看完第一強度理論的定義，大家可能會發現，第一強度理論適用于拉伸狀態材料的破壞，第一強度理論不適用于三向壓縮狀態。

莫爾-庫侖（Mohr-Coulomb）準則，也稱為第二強度理論或最大拉應變理論。

庫侖（1737-1806）在研究土和砂巖的壓縮強度后，于1773年提出：當材料的破壞沿著一定剪切平面進行時，所需的破壞力不但與剪切力有關，也與剪切面上的法向力有關。

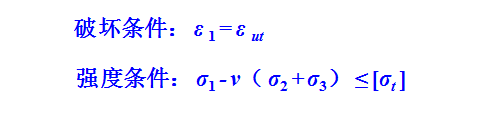
1900年德國科學家莫爾（1835-1918）將最大主應力莫爾圓引入到庫侖強度理論中，因而這個破壞準則現在被稱為莫爾-庫侖準則。

屈特加（Tresca）準則，又稱為第三強度理論或最大剪應力理論。

1864年，屈特加提出了最大剪切應力準則或稱屈特加準則。當最大剪應力達到材料所固有的某一定數值時，材料開始屈服（進入塑性變形階段），也就是說當變形體或質點中的最大切應力達到某一定值時，材料就發生屈服。

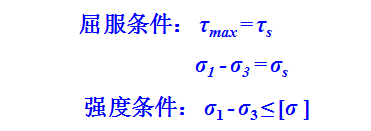
或者說，材料處于塑性狀態時，其最大切應力是一個不變的定值，該定值只取決于材料在變形條件下的性質，而與應力狀態無關，所以Tresca屈服準則又稱為最大切應力不變條件。

Tresca屈服準則不足之處就是不包含中間主應力，沒有反映中間主應力對材料屈服的影響。

范·米塞斯（van·Mises）準則，又稱為第四強度理論或最大形狀改變比能理論。

1913年，范·米塞斯考慮了變形能的作用，提出材料的屈服條件為其變形能達到某一臨界值，此即范·米塞斯準則或第四強度理論。

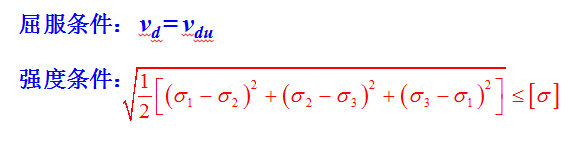
其表述是材料發生屈服是畸變能密度引起的，形狀改變能密度是引起材料屈服的因素，也即認為不論處于什么樣的應力狀態下，只要構件內一點處的形狀改變能密度達到了材料的極限值，該點處的材料就發生塑性屈服。

統一斷裂準則，也稱為橢圓斷裂準則。

2003年前后，張哲峰研究員提出了材料的統一拉伸斷裂準則。將經典的最大正應力準則、屈特加準則、范-米塞斯準則和莫爾-庫侖準則有機地統一起來。

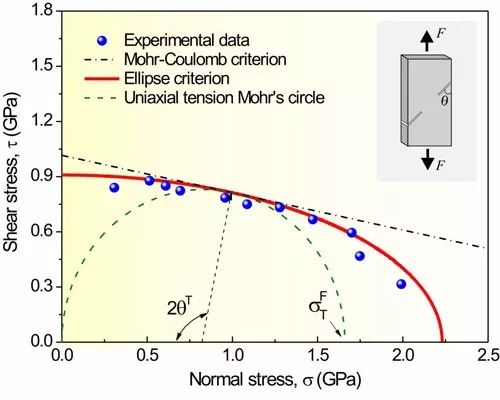
金屬玻璃拉伸斷裂的正應力效應和統一斷裂準則的實驗驗證

在該統一斷裂準則中，他認為脆性材料的拉伸破壞或者以剪切方式，或者以正斷方式，因而存在兩個臨界應力τ0和σ0，其中τ0是在剪切面上無正應力時的臨界剪切斷裂強度，而σ0是在拉伸正斷面上無剪切應力時的臨界斷裂強度。同時他定義了一個新的參數α=τ0/σ0為材料的斷裂方式因子，它是材料的特有屬性，并能控制材料剪切斷裂角的大小。

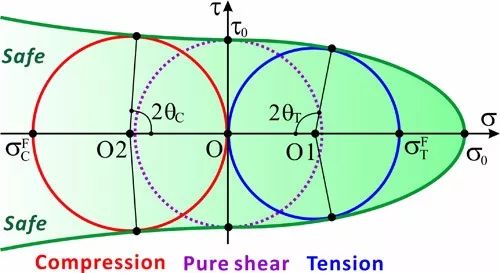
統一斷裂準則及其對金屬玻璃拉伸、壓縮及純剪切斷裂行為的描述

當α=τ0/σ0->0時，材料的剪切斷裂角接近45度，該統一準則與屈特加準則一致，也與描述單晶體屈服的施密特定律一致。

當0<α=τ0/σ0<2-1/2時，該統一準則與莫爾-庫侖準則和范·米塞斯準則是一致的；同時他發現大多數金屬玻璃材料的斷裂方式因子范圍為：1/3<α=τ0/σ0<2/3，致使其拉伸剪切斷裂通常發生在50-65度角范圍，并且具有高強度和比較小的拉伸-壓縮斷裂強度的不對稱性。

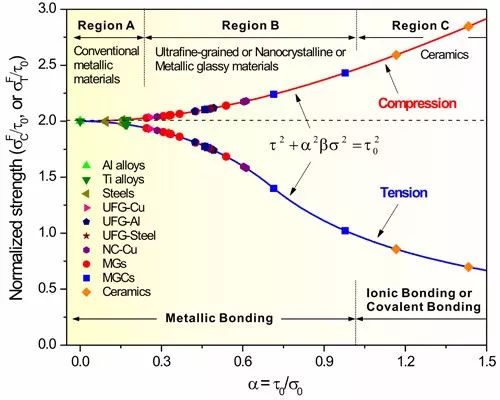
統一斷裂準則對多種材料的拉伸-壓縮強度不對稱行為的統一描述

當α=τ0/σ0>=2-1/2時，該統一準則預測材料的破壞形式為拉伸正斷，這與最大正應力準則是一致的，同時也能合理地解釋其他脆性材料嚴重的拉伸-壓縮斷裂強度的不對稱性。

從某種意義上講，上述四個經典的斷裂準則可以分別看作是該統一斷裂準則在某一種極端條件下的特殊形式，這為揭示各種不同性能材料的普遍破壞規律提供了新的參考判據。