數值模擬技術的興起

目前，國內外主要采用涂層與陰極保護技術相結合的方式來防止管道的腐蝕。但受管道所處環境復雜、管網中管道數量多、管道連接方式多樣，很難通過傳統的實地測量、室內實驗等方法來預測管道的保護效果，同時經驗公式在使用上的局限性也容易造成部分管道出現過保護或欠保護。

因此，數值模擬技術逐漸發展起來并得到了廣泛的應用，相比傳統的陰極保護設計方法，數值模擬技術可以更加準確、高效地預測被保護管道的電位分布情況以及評價陰極保護的效果。

管道陰極保護系統的數值模擬

1 簡介

管道陰極保護系統的數值模擬即對被保護管道及其所處環境進行合理假設，建立數學模型并進行求解，通過計算機的數值計算和圖像輸出，定量描述管道電位分布情況，從而達到解決問題的目的。

2 常用的數值計算方法

有限差分法（FDM）、有限元法（FEM）以及邊界元法（BEM）三種。

陰極保護體系的數學模型及邊界條件

1 分類

陰極保護體系的數學模型有分布型模型和時變型模型兩種。

2 時變型模型

時變型模型主要用于研究陰極垢層的形成以及陰極極化隨時間的變化關系，模型建立時需要考慮溫度、土壤含水量等隨時間變化的環境參數。

因為缺乏對其規律的理解，所以時變型模型的研究難度較大，目前尚沒有合適的數值計算方法，因此對陰極保護體系的研究主要集中在分布型模型上。

3 分布型模型

分布型模型主要研究陰極保護體系達到穩定狀態時管道上電位、電流分布及他們之間的關系，可用靜態場理論來分析處理。

常用數值計算方法

1 有限差分法（FDM）

20世紀60年代以來，有限差分法逐步應用到電化學計算領域中，直到80年代，Strommen等首次用有限差分法計算了陰極保護系統中被保護構件表面的電位分布，將其引入了陰極保護計算領域中。

有限差分法利用規則的網格對不規則的計算區域進行劃分，其網格劃分模型如圖1所示，復雜區域的網格生成可能占總計算時間的大部分，網格的質量對計算精度的影響很大，一般情況下，網格數越多，其得到的近似解精度越高，但當網格足夠細密時，再進一步加密網格對數值計算結果基本上沒有影響。

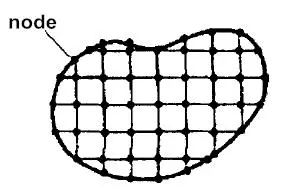
圖1 有限差分法網格劃分模型

對一維、二維計算場域，采用有限差分法所得計算結果可靠，但對于三維復雜結構的陰極保護體系來說，因有限差分法采用折線來處理不規則的邊界，容易導致計算結果不收斂、計算精度降低等問題。

因此，隨著被保護構件復雜程度的增大以及人們對計算精度要求的提高，有限差分法在陰極保護體系上的應用逐漸減少。

2 有限元法（FEM）

自20世紀70年代，有限元法逐漸被應用到管道腐蝕防護的陰極保護設計中。

有限元法是改進后的有限差分法，是變分原理在差分方法中的應用，其可用任意形狀的單元來劃分計算區域，從而便于復雜和彎曲邊界的處理，同時也提高了計算精度。

有限元法不僅能夠得到管道表面上的電位、電流分布，也可以得到某個特定范圍內的電位、電流分布情況。

有限元法的網格劃分模型如圖2所示，有限元法可以針對每個不同的單元來設置其環境參數，從而更好地貼合實際。

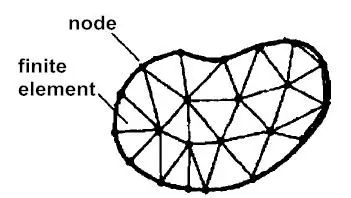
圖2 有限元法網格劃分模型

在國內，一些商業化的可用于有限元分析的軟件如COMSOL、ANSYS、FEMLAB、FEPG、ABAQUS等已廣泛的用于管道陰極保護的計算中。

目前，有限元法在管道陰極保護的設計上得到了普遍的應用，有限元法適用性強，特別適合解決幾何和物理條件比較復雜的問題，便于編制標準化程序和工程應用。但其仍存在模型計算域只能為有限域、計算量大、計算時間長等問題，在計算超長管道、結構復雜管道等的陰極保護電位時與其他方法（如邊界元法）相結合會得到更精確的結果。

3 邊界元法（BEM）

20世紀80年代，邊界元法逐步在我國得到應用，目前已經成功地用于埋地管道、海底管道以及近海石油平臺等領域，其在計算金屬表面電位分布上實現了優化設計。

邊界元法是在經典積分方程的基礎上，吸收了有限元法的離散技術而發展起來的計算方法。其基本思想是用積分方程來求解微分方程。

邊界元法的網格劃分模型如圖3所示，由于邊界元法只需要對邊界進行離散化處理，因此可將計算域的維數降低一維，從而使得輸入數據量和代數方程組的未知量大大減少，有利于計算速度和計算精度的提高。

圖3 邊界元法網格劃分模型

近幾年，邊界元法因可以將計算域進行降維處理、所需數據量小、計算時間短、計算精度高等優點得到了廣泛的關注。如由英國Computational Mechanics BEASY集團研發的BEASY CP軟件就是其中的典型代表，從應用角度來說，BEASY CP軟件具有通用性強、邊界條件設定簡單等優點。

三種數值解法的比較

以上三種方法在研究陰極保護體系，尤其是在海底管道陰極保護體系上都取得過成功，但有限差分法和有限元法的共同點是計算時必須對全部計算域進行網格劃分，致使所需數據量大、計算量大、計算精度低，而邊界元法只需對被保護管道的邊界進行網格劃分，克服了其他兩種方法的缺點，成為陰極保護設計最具前景的數值計算方法，但其無法對非均勻介質系統進行計算。

邊界元法與有限差分法以及有限元法的比較如表1所示。